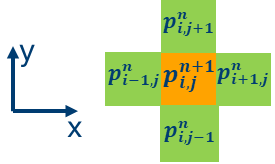サンプルコード: 等方性媒質における 2 次元有限差分波伝搬 (ISO2DFD) – インテル® oneAPI DPC++ コンパイラーの例

2020.05.27
インテル® oneAPI
DPC++

この記事は、インテル® デベロッパー・ゾーンに公開されている「Code Sample: Two-Dimensional Finite-Difference Wave Propagation in Isotropic Media (ISO2DFD) – An Intel® oneAPI DPC++ Compiler Example」の日本語参考訳です。

この記事の PDF 版はこちらからご利用になれます。

ファイル: GitHub* (https://github.com/intel/HPCKit-code-samples/tree/master/Compiler/iso2dfd_dpcpp)
ライセンス: MIT (https://github.com/intel/HPCKit-code-samples/blob/master/Compiler/iso2dfd_dpcpp/License.txt)

最適化…  
ソフトウェア:
(プログラミング言語、ツール、IDE、フレームワーク)		 インテル® oneAPI DPC++ コンパイラー (英語)
要件: C++ および DPC++ の知識

このサンプルコードによるチュートリアルは、2 次元音響等方性波動方程式を解く 2 次元有限差分ステンシルのインテル® oneAPI DPC++ コンパイラーの実装です。ダイレクト・プログラミングを使用した、インテル® DPC++ プログラミング言語の基本を示します。

必要条件

C++ プログラミングの経験と、DPC++ の基本に精通していることを前提にしています。DPC++ を利用したことのない開発者は、このチュートリアルの最後で紹介する DPC++ のリソースを参照してください。

はじめに

このチュートリアルでは、有限差分法を用いて偏微分方程式 (PDE) を解く問題を使用し、DPC++ プログラミング言語の主要機能であるキュー、バッファー/アクセサー、カーネルについて説明します (コードは GitHub* (https://github.com/intel/HPCKit-code-samples/tree/master/Compiler/iso2dfd_dpcpp) から入手できます)。これは、DPC++ でプログラミングを始める、または複雑なコードを開発および理解する参考例として使用できます。例えば、3 次元等方性波動方程式の 16 次有限差分ステンシルを実装する複雑な DPC++ の例は、GitHub* (https://github.com/intel/HPCKit-code-samples/tree/master/Compiler/iso3dfd_dpcpp) で入手できます。

多くの物理現象は PDE で表現できます。例えば波動方程式ですが、これは、特定の特性 (等方性または異方性、一定および可変密度など) を持つ媒体を伝わる波動を表します。

有限差分法を使用して、連続する PDE を一連の離散差分方程式で近似することにより、PDE の解を近似します。これは、コンピューター・システムでは反復的に求めることができます。

有限差分法で解を求められる他の PDE の例として、オプション価格設定 (数理ファイナンス)、マックスウェルの方程式 (電磁気学)、ナビエストークス方程式 (流体力学の計算) などがあります。この例で使用される単純な並列有限差分法は、上記の問題を解決するよう簡単に変更できます。

このチュートリアルでは、密度が一定の 2D 音響等方性媒体の波動方程式の解法を実装する DPC++ サンプルコードを提供します。この波動方程式は、媒体の波動伝搬をモデル化し、有限差分法 (2 次元ステンシル) を使用して解を求めます。これは、地震や石油探査における地震学、海洋音響学、レーダー画像、非破壊検査など、さまざまな分野で役立ちます。1

課題

媒体が音響でその密度が一定である場合、波動方程式 (媒体の波動伝搬を示す PDE) は次のようになります。

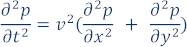
P D E describing wave propagation in the medium

ここで p は圧力、v は媒体の速度 (音波が媒体を伝搬する速度)、x と y は 2 つのデカルト座標、t は時間です。波動は、t = 0 で p によって定義される初期条件を適用して、または明示的なソース関数 s(x,y) を使用して解決できます。このサンプルコードでは明示的なソース関数を使用します。

この問題の近似解を求めるため、モデルを N x N ポイントのグリッドに分割します (簡略化のため正方形グリッドを使用しますが、長方形グリッドを使用することもできます)。∆x、∆y は、それぞれ x 軸と y 軸のグリッド内でのポイント間の距離であり、∆t は時間の増分です (時間反復は n = 0 から定義された最大反復数の範囲)。次に、2 番目の中央差分により連続偏導関数を近似することで、離散化方程式が得られます。

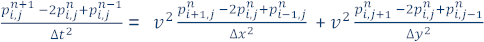
Approximation of the continuous partial derivatives using second order central differences

そして、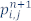 (時間 n + 1 における位置 i、j の圧力波動場の値) を解くと、2 次元音響波方程式の解を近似するため有限差分式を記述できます。

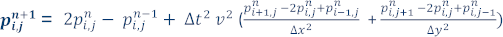
Finite-difference formula to approximate the solution of the two dimensional acoustic wave equation

これは、時間 n および n – 1 での圧力波動値に基づいた、時間 n + 1 (グリッド内のすべてのポイント) での圧力波動値を求める式です。

並列実装とサンプルコードを調査

有限差分計算でモデル化するグリッドは、規則性があるため単純なドメイン分解法の自然な候補です。これは、ここに示す明示的な差分法では特に顕著です。同時実行性を可能な限り最大化するため細かく分割します。特定の時間ステップで異なるグリッドポイントの波動場を計算するときに、データの依存関係がないためグリッドポインントごとにタスクを定義します。データの依存関係は読み取り専用である直前の時間ステップの隣接するグリッドポイントでのみ存在するため、グリッドのすべてのポイントは反復ごとに独立して更新できます。

それぞれの反復における 2 次元グリッドの各ポイントは、次のステンシルのグラフが表すように、上記の式を使用して更新できます。圧力波動場の更新値はオレンジ色で、隣接するグリッドポイントは緑色です。

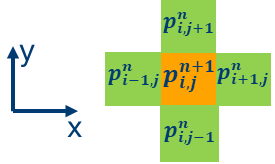
Grid representation of finite difference scheme

このサンプルコードでは、更新は iso_2dfd_iteration_global 関数に含まれています。

// グローバル id (gid) で指定される位置のグリッドポイントを更新するステンシルコード。
// グリッドポイントの新しい時間ステップは、水平方向と垂直方向の両方で
// 隣接する値と、以前の時間のグリッドポイントの値に基づいて計算されます。
value = 0.0;
value += prev[gid +  1] - 2.0*prev[gid] + prev[gid-1];
value += prev[gid + nCols] - 2.0*prev[gid] + prev[gid - nCols];
value *= dtDIVdxy * vel[gid];
next[gid] = 2.0f*prev[gid] - next[gid] + value;

これは、サンプルコードで定義されるカーネル関数のコア部分であり、ステンシル計算がどのように行われているかを説明します。

main() 関数

始めに main 関数から見ていきます。4 つの 1 次元配列が定義され割り当てられています。

int main(int argc, char* argv[]) {

  float* prev_base;
  float* next_base;
  float* next_cpu;
  float* vel_base;
<

これらの配列のうち 3 つはカーネル関数の波面を更新するために使用されます。prev_base と next_base は、それぞれ反復 n と n + 1 での圧力波面を表し、vel_base は中速を格納します。next_cpu 配列は、next_base 配列と同等であり、ホストで実行される同じ計算と比較して、デバイスでの計算を検証します。

割り当てられたこれらの配列は、パラメーターとして initialize 関数に渡されます。初期化関数は、波面配列と速度配列を初期化して、ソース関数を prev_base 配列に追加します。ここで使用するソース関数は、地震データ処理で一般的に使用される離散化されたリッカー・ウェーブレットです。

// 配列を初期化し、初期条件を設定 (ソース)
initialize(prev_base, next_base, vel_base, nRows, nCols);

DPC++ デバイスセレクター、キュー、およびバッファー

これは標準 C++ コードです。device_selector オブジェクトで指示されるデバイスやアクセラレーターで実行されるワークをキューに投入するため使用するデバイスキューを作成する際に、DPC++ の機能を使用します。

// デバイスセレクターを'host'、'GPU’または 'default' として定義
gpu_selector device_selector;
// default_selector device_selector;

// デバイスキューを作成
queue q(device_selector, [&](exception_list eL) {

特定のデバイスにワークを送信するデバイスキューを作成できます。例えば、ここで示すように GPU セレクターを使用して GPU にワークをエンキューしたり、実行時にデバイスを選択するデフォルトセレクターを利用することもできます。

次のステップは、ホストとデバイス間でデータを通信するバッファー・オブジェクトを作成することです。バッファーには、1 次元、2 次元、または 3 次元の要素コレクションを格納できます。ここでは、float 型の 1D 配列へ格納します (2D グリッドを表現するため 1D 配列を使用)。バッファーは、C または C++ の配列に直接関連付けられているため、圧力波動場の更新計算で使用される 3 つの配列に接続されています。これらのバッファーのデータはホストとデバイス間でやり取りできます。

buffer<float, 1> b_next(next_base, range<1>{nsize});
buffer<float, 1> b_prev(prev_base, range<1>{nsize});
buffer<float, 1> b_vel(vel_base, range<1>{nsize});

ここでは、float 配列ごとに 1 つのバッファーが宣言され、バッファーサイズは nsize 要素の 1D 範囲であることを示しています。

// グリッドの合計サイズを計算
size_t nsize = nRows * nCols;

コマンドハンドラーとカーネル定義

この時点で、時間ステップを反復するループを作成します。このループは、すべてのグリッドポイントで圧力波動場の値を更新します。

// 時間ステップ全体で反復
for (unsigned int k = 0; k < nIterations; k += 1){

    // 実行するコマンドグループを送信
    q.submit([&](handler &cgh) {

反復ごとに、上記で作成したデバイスキューにコマンドグループを送信することに注意してください。コマンドグループには、キューで定義されるデバイスにエンキューされるカーネル関数が含まれます。

このコマンドグループは、実行時に構築され、カーネル実行に必要なすべての要件を含む cgh コマンド・グループ・ハンドラーをパラメーターとして取得します。ここでは、以前のステップで GPU セレクターでデバイスキューを作成しているため、GPU にあります。

また、以前のステップで、ホストとデバイス間で共有するデータを保存するため、ホストにバッファーを作成しました。ここでは、デバイスのバッファーからデータにアクセスするアクセサーを作成します。このアクセサーは、デバイスで使用されるメモリー・オブジェクトへのポインターとして機能し、上記で定義されたバッファーを介してホストとの間でデータをやり取りするため、カーネル関数で使用されます。

auto next = b_next.get_access<access::mode::read_write>(cgh);
auto prev = b_prev.get_access<access::mode::read_write>(cgh);
auto vel  = b_vel.get_access<access::mode::read>(cgh);

アクセサーのアクセスモードは、波動場の伝搬に使用されるバッファー (b_next と b_prev) では読み取りと書き込みの両方であることに注意してください。これは、このバッファーが時間ステップごとに更新されるためです。

次のステップでは、カーネル関数の実行範囲を定義します。この例では、2 次元の範囲でワークアイテムのコレクション (カーネル関数のインスタンスを実行) を定義し、すべてのワークアイテムがカーネル関数のインスタンスを実行します。

ここでは、グリッドサイズ (入力引数 nRows と nCols で指定) により範囲を定義しています。

auto global_range = range<2> (nRows, nCols);

range 内の各ワークアイテムは、次のコードで示すように、item<2> 型の値で識別されます。ここで、ワークを実行するためデバイスに送信します。DPC++ では、parallel_for 関数を使用してデバイスで実行するカーネル関数を送信できます。このカーネル関数は、C++ ラムダ関数の構文を使用して構築されます。C++ 11 以降では、呼び出された場所で関数オブジェクトを定義するラムダ式を使用できます。

この parallel_for 関数は、カーネル関数のインスタンス (グローバル範囲とローカル範囲) をいくつか作成し、それらをコマンドキューに追加してデバイスで並列実行します。

cgh.parallel_for<class iso_2dfd_kernel>(
    range<2>{global_range, [=](item<2> it) {
      iso_2dfd_iteration_global(it, next.get_pointer(),
            prev.get_pointer(), vel.get_pointer(),
            dtDIVdxy, nRows, nCols);
    });

parallel_for 関数の最初のパラメーターは、カーネル関数で実行される範囲を定義します。これは、グローバル範囲で指定します。item<2> 型の 2 番目のパラメーターは、各カーネル呼び出しのインデックス、または ID です。このパラメーターは、デバイスで実行されるカーネルのすべてのインスタンスが一意の識別子を持つことを保証します。また、テンプレート・パラメーター <class iso_2dfd_kernel> は、カーネルとホストコードを連携させるために使用されます。カーネルは C++ ラムダ関数構造によって定義されており、C++ のラムダ関数にはカーネルをホストコードにリンクするのに使用できる名前がないため、クラス名を追加する必要があります。

上記のコード例では、カーネル関数の本体が parallel_for 関数によって作成されるカーネル関数のすべてのインスタンスで並列実行されるコードを定義しています。ここでは、iso_2dfd_iteration_global() 関数呼び出しがそれにあたります。この関数は、パラメーター it で指定されるグリッドポイントの圧力波動場を更新します。これは、デバイスで実行されるカーネル関数のインスタンスを一意に識別 (インデックス付け) します。

iso_2dfd_iteration_global() 関数を説明する前に、各反復で、next ポインターと prev ポインターを効率良く入れ替える if-else 文がコードに含まれる理由を理解することが重要です。

if (k % 2 == 0)
   cgh.parallel_for<class iso_2dfd_kernel>(
       range<2>{global_range}, [=](item<2> it) {
         iso_2dfd_iteration_global(it, next.get_pointer(),
               prev.get_pointer(), vel.get_pointer(),
               dtDIVdxy, nRows, nCols);
       });
else
   cgh.parallel_for<class iso_2dfd_kernel_2>(
       range<2>{global_range}, [=](item<2> it) {
         iso_2dfd_iteration_global(it, prev.get_pointer(),
               next.get_pointer(), vel.get_pointer(),
               dtDIVdxy, nRows, nCols);
       });

これは、3 つではなく 2 つの配列を更新に使用できるようにするするためです。すべての反復で配列を入れ替えることにより、圧力波動場を保持するため 3 つ目の配列を割り当てる必要がなくなります 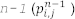。これは、波動場で更新される配列から情報を読み取ることが可能であるためです 。

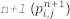iso_2dfd_iteration_global() 関数は、パラメーター it で指定されるグリッドポイントの圧力波動場を更新します。この関数では、ローカルとグローバル・インデックスを (item<2> 型の) パラメーター it から取り出す方法を示します。

void iso_2dfd_iteration_global(item<2> it, float *next, float *prev, 
           float *vel, const float dtDIVdxy, int nRows,
           int nCols) {

  float value = 0.0;
  // グローバル id を計算。
  // item 変数の get.global.id() 関数を使用してグローバル id を計算できます。
  // 2 次元配列はメモリー内で行優先順に配置されます。
  size_t gidRow = it.get_id(0);
  size_t gidCol = it.get_id(1);
  size_t gid = (gidRow)*nCols + gidCol;

いくつかの方法でグローバル ID (gid) を計算できます。上記は、item クラスのメンバー関数を使用する用例を示します。

最後のステップではステンシル計算を再確認します。次のコードでは if 文を使用して、最初に配列境界で更新が行われていないことを確認する必要があります。ここでの差分ステンシルは、隣接するグリッドポイントの値を使用して 1 つのグリッドポイントを更新します。そのため、配列境界にあるグリッドポイント (halo) が更新されていないことを確認して、セグメンテーション・エラーを回避する必要があります。定数 HALF_LENGTH は、ステンシルサイズの半分 (この場合 2) を格納することに注意してください。

グリッドポイントを更新する計算には、gid 変数値をインデックスとして使用します。カーネル関数のすべてのインスタンスがグリッド内の 1 つのポイントを更新するため、これがどれくらい細粒度のドメイン分解であるか分かります。

// 2 次元波動方程式を求める計算。
//  gid が (halo ではなく) 有効なグリッド内にあるか確認
if ((gidCol >= HALF_LENGTH && gidCol < nCols - HALF_LENGTH) &&
    (gidRow >= HALF_LENGTH && gidRow < nRows - HALF_LENGTH) )
   {
    // グローバル id (gid) で指定される位置のグリッドポイントを更新するステンシルコード。
    // グリッドポイントの新しい時間ステップは、水平方向と垂直方向の両方で
    // 隣接する値と、以前の時間のグリッドポイントの値に基づいて計算されます。
         value = 0.0;
         value += prev[gid +  1] - 2.0*prev[gid] + prev[gid-1];
         value += prev[gid + nCols] - 2.0*prev[gid] + prev[gid - nCols];
         value *= dtDIVdxy * vel[gid];
         next[gid] = 2.0f*prev[gid] - next[gid] + value;
    }

これでコードの調査は完了しました。

この記事の最初にあるリンクをクリックすると、完全なサンプルコードをダウンロードできます。このサンプルコードは学習用途のみに使用され、DPC++ 基本構造の使用を明示的に示すようには最適化されていないことに注意してください。このコードは、DPC++ の基本的な機能を理解することを目的としており、DPC++ を使用したコード開発の開始点として参照できます。

コードをコンパイルして実行

Linux* でコードをコンパイルして実行するには、インテル® oneAPI 向けの環境変数を設定します。以下に例を示します。

source <oneAPI install dir>/setvars.sh

サンプルコードがあるディレクトリーで次のコマンドを実行します。

mkdir build
cd build
cmake ..
make -j

実行するには次のように入力します。

make run

あらかじめ選択されたパラメーターで実行ファイルを実行します。

次のように各種パラメーターを指定してコードを実行することもできます。

./iso2dfd 1000 1000 2000

上記のコマンドは、1000 x 1000 のグリッドサイズで iso2dfd 実行ファイルを実行し、2000 時間ステップ以上反復します。

ここでの実行では、システムにインテル® プロセッサー・グラフィックス Gen9 が搭載されていることを前提としています。Gen9 が存在しない場合、コード内の device_selector 宣言を default_selector に変更します。これにより、GPU が存在しない場合 CPU をデバイスとして使用できます。

//gpu_selector device_selector;
default_selector device_selector;

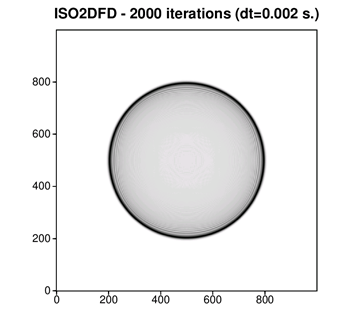
実行出力は、次の図のような波動場になります。これは、正方形グリッドの中央にある光源から伝わる円形の波面を表しています。これは、地震波動フィールドを表示するユーティリティーである John Stockwell の SeisUnix GitHub* アーカイブ (英語) からダウンロードできる SU 地震処理ライブラリーを使用して .iso2dfd の出力を表示しています。

次の図は別の出力例を示しています。ここでは 2 層モデルを定義し (図の左部分で示すように、モデル上部の音響波速度は 3000 ミリ/秒、下部の速度は 1500 ミリ/秒です)、時間反復の総数を変えてコードを複数回実行します。このようにして、モデルの高速部分と低速部分で波動 (およびモデルのエッジと 2 つのレイヤー間のインターフェイスの反射と屈折) が時間内に伝搬するスナップショットを取得できます。

まとめ

このチュートリアルでは、2 次元音響等方性波動方程式を解く 2 次元有限差分ステンシルの並列実装について説明しました。完全なサンプルコードは GitHub* (https://github.com/intel/HPCKit-code-samples/tree/master/Compiler/iso2dfd_dpcpp) からダウンロードできます。これは、簡素でありながら実際のアプリケーションで DPC++ プログラミング言語の基本要素を示すことを目標としています。さらに複雑なアプリケーション開発に向けた開始点として活用してください。特に「関連情報」で引用する「16 次ステンシルを使用した 3D 等方性波動伝搬問題」のような、複雑な有限差分ステンシル並列コードを理解するのに役立ちます。

関連情報

インテル® oneAPI ツールキット (英語) のサイトには、DPC++ およびインテル® oneAPI ツールキットの詳しい説明があります。

その他のドキュメントとサンプルコードについては、https://software.intel.com/oneapi/documentation の注目のドキュメントを参照してください。

ISO3DFD DPC++ サンプルコード (https://github.com/intel/HPCKit-code-samples/tree/master/Compiler/iso3dfd_dpcpp) は、16 次ステンシルを使用した 3D 等方性波動伝搬問題のさらに高度なソリューションです。

参考資料

  1. Villarreal, A., & Scales, J. A. (1997). Distributed three-dimensional finite-difference modeling of wave propagation in acoustic media. Computers in Physics, 11, 388.

製品とパフォーマンス情報

1インテル® コンパイラーでは、インテル® マイクロプロセッサーに限定されない最適化に関して、他社製マイクロプロセッサー用に同等の最適化を行えないことがあります。これには、インテル® ストリーミング SIMD 拡張命令 2、インテル® ストリーミング SIMD 拡張命令 3、インテル® ストリーミング SIMD 拡張命令 3 補足命令などの最適化が該当します。インテルは、他社製マイクロプロセッサーに関して、いかなる最適化の利用、機能、または効果も保証いたしません。本製品のマイクロプロセッサー依存の最適化は、インテル® マイクロプロセッサーでの使用を前提としています。インテル® マイクロアーキテクチャーに限定されない最適化のなかにも、インテル® マイクロプロセッサー用のものがあります。この注意事項で言及した命令セットの詳細については、該当する製品のユーザー・リファレンス・ガイドを参照してください。

注意事項の改訂 #20110804

タイトルとURLをコピーしました