この記事は、Intel Tech.Decoded で公開されている「Toward Accurate and Highly Performant Simulations with BRODA® SOBOL Quasi-random Number Generator」(https://techdecoded.intel.io/resources/toward-accurate-and-highly-performant-simulations-with-broda-sobol-quasi-random-number-generator/) の日本語参考訳です。
この記事の PDF 版はこちらからご利用になれます。
擬似乱数ジェネレーターは、さまざまな AI アルゴリズム (例: 粒子群の最適化) や、金融やリスク管理でよく使用される擬似モンテカルロ・シミュレーションにおいて、不一致度の低い乱数列のソースとして広く使用されています。BRODA 社が開発した SobolSeq65536 ジェネレーターが生成する Sobol’ 数列は、数値積分の収束性を高める一様性条件 (特性 A と特性 A’) を満たしており、既存の疑似乱数ジェネレーターよりも速度と精度の両方において優れています [2]。
インテル® oneAPI マス・カーネル・ライブラリー (インテル® oneMKL) は、インテルベースのシステムで最も高速で、最も多く使用されている数学ライブラリーです。演算処理ルーチンを高速化し、アプリケーションのパフォーマンスを向上させ、開発期間を短縮します [5]。SobolSeq65536_MKL は、SobolSeq65536 数列ジェネレーターにインテル® oneMKL が組み込まれたものです。SobolSeq65536_MKL は、同じ統計的性質になるように SobolSeq65536 の方向比を使用しています。インテル® oneMKL は、インテル・ハードウェア上で大規模シミュレーションに不可欠な BRODA の SOBOL の数列生成パフォーマンスを大幅に向上させるとともに、インテル® Xe グラフィックス・ハードウェア上でインテル® oneMKL DPC++ API を用いて SobolSeq65536 ジェネレーターを実行できるようにしました。
SobolSeq65536 と SobolSeq65536_MKL ジェネレーターの統計的性質
SobolSeq65536 ジェネレーターによって生成される不一致度の低い Sobol’ 数列は、既存のジェネレーターの出力数列よりも統計的性質が優れています [2]。有名な金融ベンチマークの「ヨーロッパ型オプションの価格付け」と「アジア型オプションの価格付け」について、S. Joe 氏と F. Y. Kuo [3] (Joe & Kuo) 氏の方向比で BRODA の SobolSeq65536 ジェネレーターと Sobol’ 数列ジェネレーターを比較した結果を以下に示します。
次のパラメーターでヨーロッパ型コールオプションの価格付けについて考えます: S0 = 100、K= 100、 = 0.0、 = 0.2、T = 1y。アット・ザ・マネー (ATM) コールの理論的なブラック-ショールズ価格は 7.965667455 です。標準的なアルゴリズムでは、オプションの価格は次の d 次元の積分として表されます。
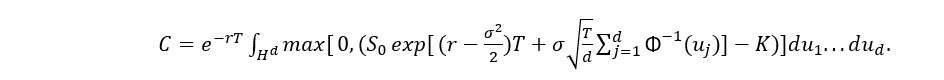
「アジア型オプションの価格付け」では、次のパラメーターで幾何平均アジア型コールオプションの価格付けについて考えます: S0 = 100、K= 100、 = 0.05、 = 0.2、T = 0.5y。標準的なアルゴリズムでは、幾何平均アジア型コールオプションの価格は次の d 次元の積分として表されます。
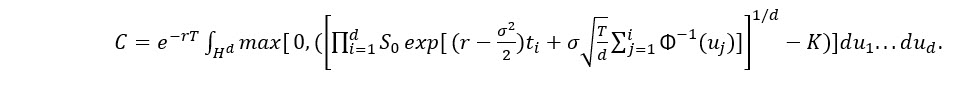
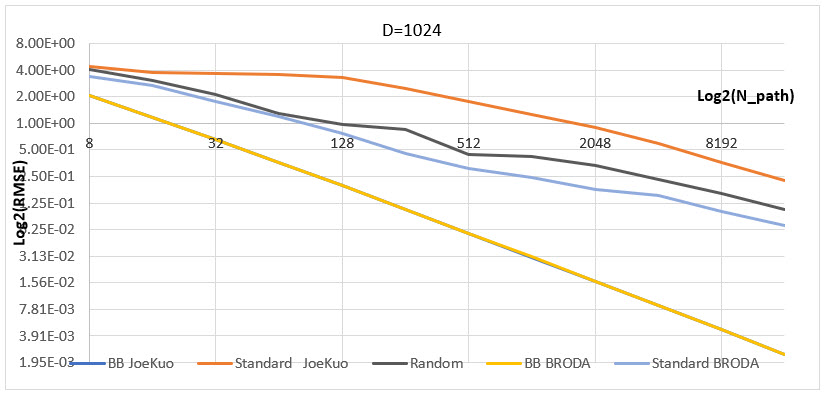
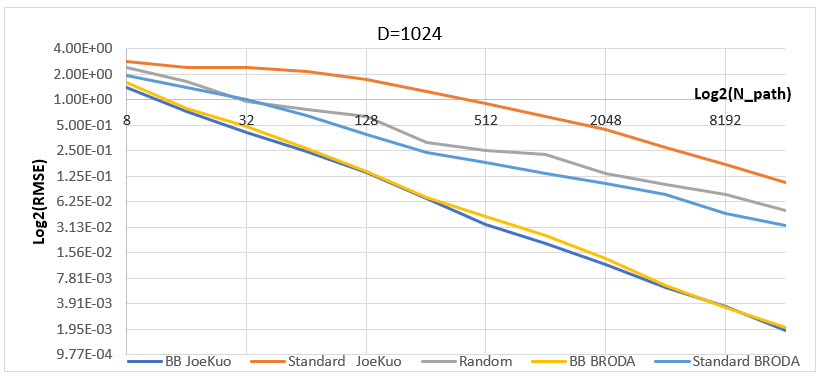
「ヨーロッパ型オプションの価格付け」と「アジア型オプションの価格付け」のベンチマークにおける、2 乗平均平方根誤差 (RMSE) の積分結果 (20 回の実行の平均) を以下に示します (次元 d =1024)。
BRODA と Joe & Kuo のジェネレーターを比較すると、Standard 方式の場合 Joe & Kuo は BRODA よりもはるかに効率が悪く、乱数ジェネレーター (MC 方式) よりも効率が悪いことが分かります。Brownian bridge (BB) の場合、どちらのジェネレーターも同様のパフォーマンスを示します。
インテル® oneMKL によるパフォーマンスの高速化
インテル® oneMKL のベクトル統計コンポーネントは、Sobol’ 擬似乱数ジェネレーターの実装 (インテルの CPU と Xe グラフィックスをサポート) を含む、一般的な乱数ジェネレーターのセットを提供します。Sobol’ 擬似乱数ジェネレーターの実装も、初期化時にユーザー定義のパラメーターの登録を受け付けます。これに基づいて、インテル® oneMKL を BRODA の SobolSeq65536 ジェネレーターに統合しました。
SobolSeq65536_MKL (インテル® oneMKL が統合された SobolSeq65536) には、ポイントごとにアクセスする「シングルポイント」バージョンと 1 回の関数呼び出しでいくつかの SOBOL ベクトルを取得できる「ブロック」バージョンがあります。
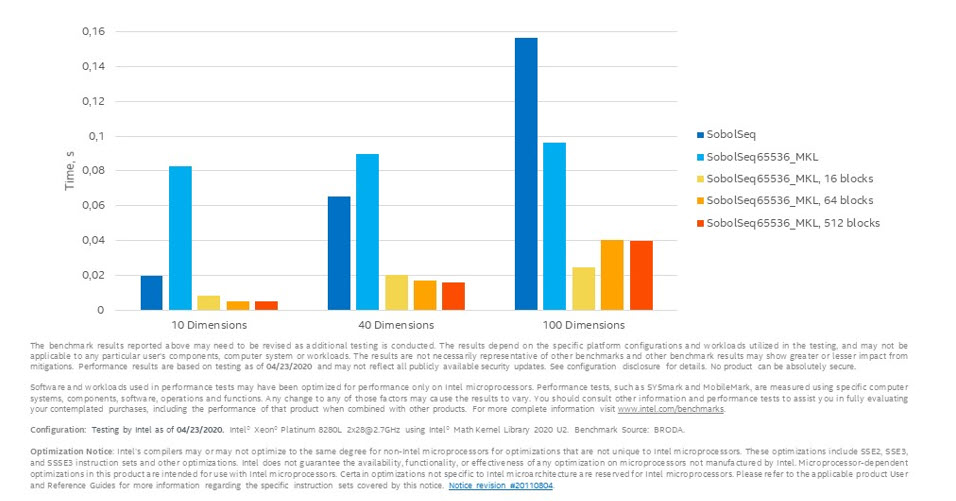
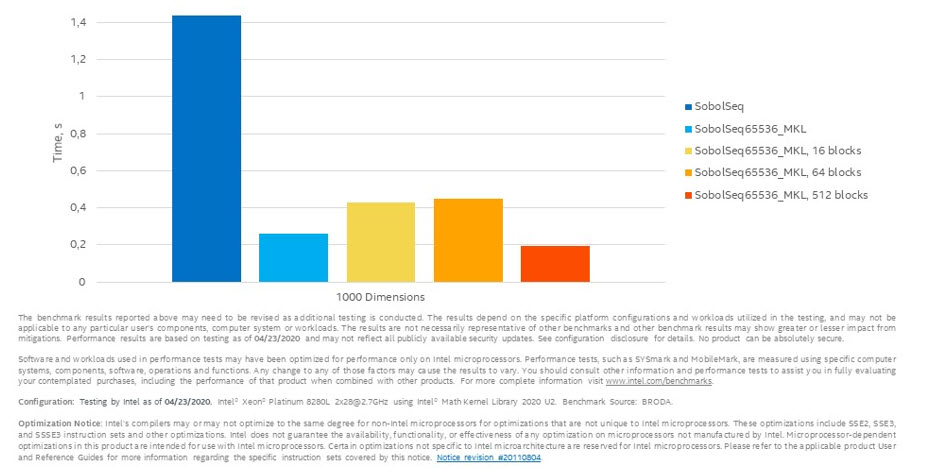
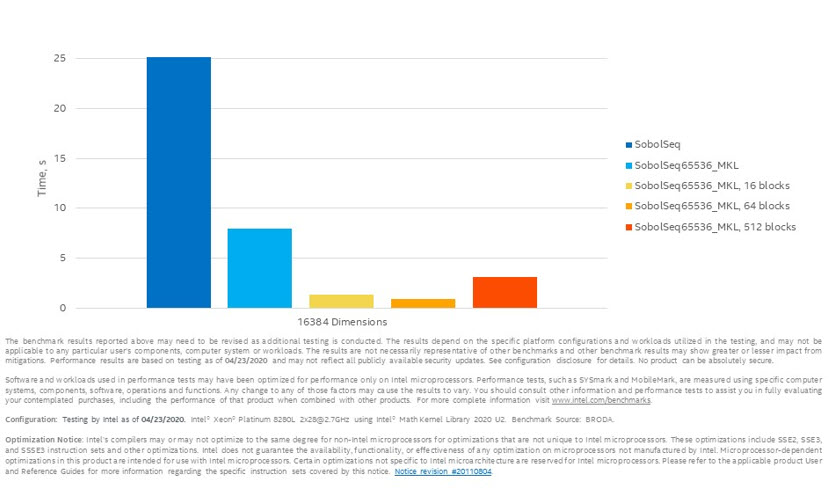
SobolSeq65536 と SobolSeq65536_MKL で 2^20 個の疑似乱数を生成したパフォーマンス (10 回の実行の平均) を図 3 に示します。
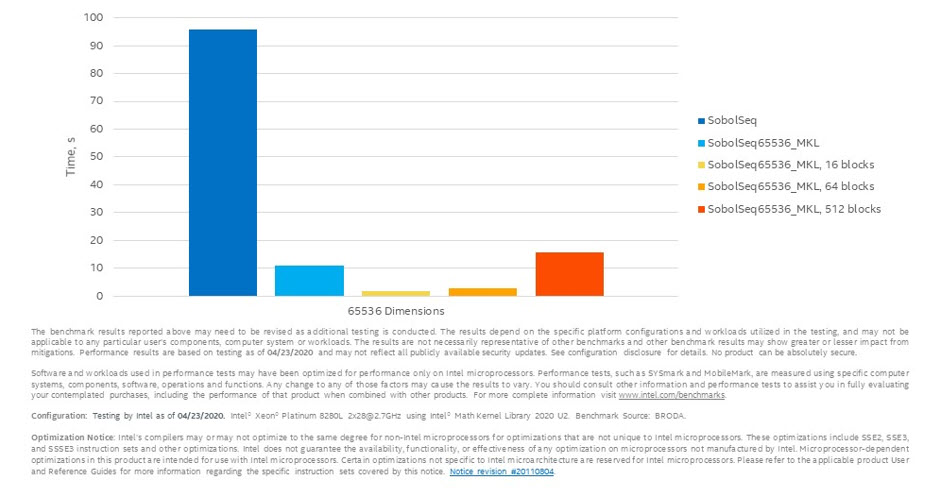
図 3. SobolSeq65536 と SobolSeq65536_MKL のパフォーマンス比較
グラフから、SobolSeq65536_MKL の「ブロック」バージョンは SobolSeq65536 のパフォーマンスを大きく上回っていることが分かります。SobolSeq65536_MKL は SobolSeq65536 と比較して、10 次元で 4 倍、100 次元で 4 倍、1000 次元で 7.9 倍、16384 次元で 27.7 倍、65535 次元で 52.7 倍のスピードアップを達成しました。
まとめ
BRODA の SobolSeq65536 ジェネレーターは不一致度の低い 65536 次元の Sobol’ 数列ジェネレーターで、速度と数列の統計的性質の両方において既存のジェネレーターを上回っています。SobolSeq65536_MKL は、SobolSeq65536 数列ジェネレーターにインテル® oneMKL が組み込まれたものです。 SobolSeq65536_MKL ジェネレーターの「ブロック」バージョンは、インテル・ハードウェアのベクトル化機能を利用できるため、「シングルポイント」バージョンと比較して大幅なパフォーマンス向上が見られました。
参考資料
[1] BRODA Ltd. http://www.broda.co.uk (2020). [2] Sobol’ I., Asotsky D., Kreinin A., Kucherenko S. Construction and Comparison of High-Dimensional Sobol’ Generators, Wilmott, Nov:64-79, 2011, http://www.broda.co.uk/doc/HD_SobolGenerator.pdf [3] Joe S., Kuo FY. Constructing Sobol sequences with better two-dimensional projections. SIAM Journal on Scientific Computing. 2008;30(5):2635-54. [4] Bianchetti M., Kucherenko S., Scoleri S., Pricing and Risk Management with High-Dimensional Quasi Monte Carlo and Global Sensitivity Analysis, Wilmott, July, pp. 46-70, 2015, http://www.broda.co.uk/doc/PricingRiskManagement_Sobol.pdf [5] Intel® oneAPI Math Kernel Library – https://software.intel.com/content/www/us/en/develop/tools/math-kernel-library.html [6] Intel® oneAPI Math Kernel Library Vector Statistics – Sobol quasi-random number generator. https://software.intel.com/content/www/us/en/develop/documentation/mkl-vsnotes/top/testing-of-basic-random-number-generators/basic-random-generator-properties-and-testing-results/sobol.html製品とパフォーマンス情報
1実際の性能は利用法、構成、その他の要因によって異なります。詳細は、www.Intel.com/PerformanceIndex (英語) を参照してください。