この記事は、インテル® デベロッパー・ゾーンに公開されている「Improve Performance with Vectorization」(https://software.intel.com/en-us/articles/improve-performance-with-vectorization) の日本語参考訳です。
この記事の PDF 版はこちらからご利用になれます。
この記事では、ベクトル化によりソフトウェアのパフォーマンスを向上する手順を説明します。ベクトル化の手順を説明するため、アプリケーション全体の例と簡単な例が含まれています。ハードウェアのコア数が増加し、ベクトルレジスターの幅が広くなるとともに、ハードウェアの進歩に合わせて高レベルの並列処理とベクトル化が行われるように、ソフトウェアを現代化したり変更する必要があります。この向上したパフォーマンスにより、複雑な問題を効率良く解くことができます。前の記事「ベクトル化のパフォーマンスの認識と測定」 (https://software.intel.com/en-us/articles/recognizing-and-measuring-vectorization-performance) では、ソフトウェアのベクトル化の効率を測定する方法について説明しました。
この記事では、「SIMD」と「ベクトル化」は同じ意味で使用されます。はじめに、ベクトル化の概要を説明します。SIMD は Single Instruction Multiple Data の略で、同じ命令を複数のデータ要素で同時に使用します。インテル® アドバンスト・ベクトル・エクステンション 512 (インテル® AVX-512) は、512 ビット幅のレジスターを利用できます。これらのレジスターには、8 つの倍精度浮動小数点値、16 の単精度浮動小数点値、または 16 の整数を格納できます。レジスターを完全に利用すると、8 から 16 の値 (値の型および使用される命令に依存します) を同時に演算する 1 つの命令が適用されます。
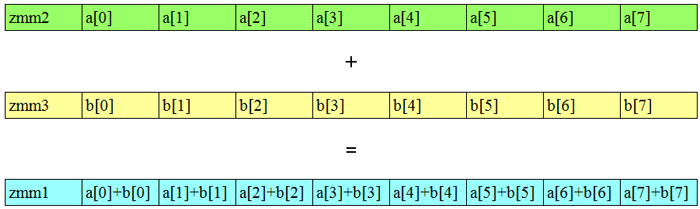
図 1: インテル® AVX-512 の zmm レジスターにおける SIMD 演算の例
インテル® AVX-512 レジスターのすべての利用可能なレーンにデータが格納された場合、パフォーマンスはスカラー演算の 8 倍から 16 倍になります。一般に、多くのスカラー演算、シャッフルおよびデータ移動が行われるため、(パフォーマンスは大幅に向上しますが) アプリケーション全体のスピードアップは 8 倍から 16 倍には達しません。インテル® アドバンスト・ベクトル・エクステンション 2 (インテル® AVX2) およびインテル® アドバンスト・ベクトル・エクステンション (インテル® AVX) 命令はインテル® AVX-512 命令の幅の半分で、インテル® ストリーミング SIMD 拡張命令 4 (インテル® SSE4) 命令はインテル® AVX およびインテル® AVX2 命令の幅の半分です。これらはすべてパフォーマンス・レベルの向上につながります。
ベクトル化によるソフトウェアのパフォーマンス・レベルの向上
ソフトウェア開発者はスカラーコードからベクトルコードにどのように移行すればいいのでしょうか。従うべき手順を次に示します。
- ベクトル化されたライブラリー (例えば、インテル® マス・カーネル・ライブラリー (インテル® MKL)) を使用する
- SIMD を考慮する (反復または複数回行われる処理を考慮する)
- パフォーマンス解析 (データを収集して改善) を行う
- SIMD で表現する
最初の 3 つの手順は、前述の https://software.intel.com/en-us/articles/recognizing-and-measuring-vectorization-performance で説明しています。この記事では、SIMD での表現とコードの変更について説明します。次の項目があります。
- プラグマとディレクティブの使用
- SIMD 対応関数の記述
- ループ不変依存関係の削除
- 一時変数のショートベクトルへの展開
- データのアライメントに関する注意
- データレイアウトの向上
プラグマ/ディレクティブと依存関係
コンパイラーは優れた自動ベクトル化機能を備えていますが、繰り返し do ループ内部のメモリー参照を一義化できない (ループ反復と別の反復の間に依存関係がないことを保証できない) 場合もあります。コンパイラーがデータの依存関係を判断できない場合、スカラーコードが生成されます。コンパイラーの解析が非常に複雑になった場合も、ベクトル化されずスカラーコードが生成されます。
ベクトル化を向上する最も一般的な手法は、プラグマまたはディレクティブの追加です。コンパイラーのプラグマ (C/C++) またはディレクティブ (Fortran) は、コード単独で識別できるよりも詳細なコードセグメントに関する情報をコンパイラーに提供して、コンパイラーがより多くの最適化を行えるようにします。プラグマやディレクティブが適用される最も一般的な例は、for ループや do ループをベクトル化しても安全かどうか判断できないポインターの一義化です。do (または for) ループに入るデータがオーバーラップしないことが分かっている場合は、プラグマまたはディレクティブを追加して、可能性のある依存関係を無視してベクトル化するようにコンパイラーに指示できます。
異なるコンパイラー開発元により、さまざまなプラグマ/ディレクティブが実装されました。データ依存の可能性を無視するようにコンパイラーに知らせることは非常に一般的であるため、ソフトウェア開発者にとっては、各コンパイラー独自のプラグマを利用するのではなく、すべてのコンパイラーで認識できるプラグマやディレクティブを利用するほうが便利です。OpenMP* 委員会は、2013 年の OpenMP* 4.0 仕様に SIMD コンパイラー・プラグマ/ディレクティブを追加することにより、その隙間を埋めました。標準化されたプラグマ/ディレクティブを使用すると、多くのコンパイラーでそのまま利用できます。
このプラグマ/ディレクティブの構文は次のとおりです。
#pragma omp simd !$omp simd
ほかにも役立つ SIMD プラグマの追加オプションがあります。
safelen(length),linear(list:linear-step),aligned(list[alignment]) , . . .
これらの追加パラメーターは、コードに次のような反復が含まれる場合に役立ちます。
for (i=8;i<n;i++) {
. . .
x[i] += x[i-8]* . . . ;
. . .
}
これらの反復間には依存関係があります。しかし、安全な長さであるため (依存関係により 8 つの値のみ戻る)、コンパイラーは長さが 8 の SIMD を安全にベクトル化することができます。この場合、次のようにオプション・パラメーター使用します。
#pragma omp simd safelen(8)
SIMD プラグマ/ディレクティブを使用すると、プログラムおよびデータアクセスを十分に理解し、依存性がないと仮定しても安全であるとコンパイラーに知らせていることになります。この仮定が間違っていると、正しい結果は得られません。一部の開発者がサニティーチェックに利用する簡単な手法 (ループの順序を逆にする) もありますが、結果が正しいことは保証されません。ループの順序を逆にして値が変わる場合、コードを変更しないでベクトル化やスレッド化を行うことは安全ではありません。コードを安全にベクトル化するには、safelen やアトミック操作のような追加のオプション、あるいはほかの実行制御が必要になります。
結果が正しい場合、そのデータセットでは演算の順序は問題ではありません。しかし、異なるデータセットでは演算の順序が問題になる可能性があります。そのため、チェックに失敗した場合に依存関係があることは明白ですが、チェックをパスしても安全性は保証されません。インテル® Advisor などのツールは、より正確な解析を提供し、依存関係を特定できるように支援します。また、安全に SIMD プラグマやディレクティブを適用するヒントを示します。
関数
ループ内の頻繁な関数/サブルーチン呼び出しはベクトル化を妨げます。この問題の解決策はいくつかあります。例えば、ショート関数はベクトル化可能な関数として記述できます。多くの超越関数のベクトルバージョンは、コンパイラーとともに提供される数学ライブラリーに含まれています。適切な構文を使用すると、コンパイラーはユーザーが記述した関数のベクトルバージョンとスカラーバージョンの両方を生成します。
数を 2 乗して、値に定数を加える関数を記述してみましょう。関数は次のようになります。
double sqadd(double a, double r) {
double t ;
t = a*a + r ;
return(t) ;
}
この関数のベクトルバージョンとスカラーバージョンを生成するようにコンパイラーに伝えるには、次のように記述します。
#pragma omp declare simd // ベクトルバージョンを生成するようにコンパイラーに伝える
double sqadd(double a, double r) {
double t ;
t = a*a + r ;
return(t) ;
}
次に、関数を呼び出している場所でも、次のように記述してループをベクトル化するようにコンパイラーに指示します。
#pragma omp simd // ループが関数を呼び出している場合でもベクトルコードを生成するようにコンパイラーに指示する
for (i=0 ; i<n; ++) {
. . .
anarray[i] = sqadd(r, t) ;
. . .
}
Fortran では、次のディレクティブを使用します。
!$omp declare simd(subroutine name)
例えば、Fortran で上記の関数のベクトル化可能な実装を生成するには、次のように記述します。
real*8 function sqadd(r,t) result(qreal)
!$omp declare simd(sqadd)
real*8 :: r
real*8 :: t
qreal = r*r + t
end function sqadd
関数を呼び出すファイルで、次のように定義します。
INTERFACE
real*8 function sqadd(r,t)
!$omp declare simd(sqadd)
real*8 r
real*8 t
end function sqadd
END INTERFACE
コンパイラーは、sqadd の呼び出しを含む do ループをベクトル化します。モジュールが使用され、関数やサブルーチンが SIMD 対応として宣言されている場合、そのモジュールを使用するファイルは関数/サブルーチンが SIMD 対応であることを認識して、ベクトル化されたコードを生成します。Fortran での SIMD 関数/サブルーチンの作成についての詳細は、Fortran の明示的なベクトル・プログラミング (英語) を参照してください。
ループ不変依存関係
do/for ループ内に条件がループ内で変わらない if/else 文が記述されていると、条件付きのためベクトル化が妨げられることがあります。この場合は、ベクトル化できるようにコードを変更します。例えば、次のようなコードの場合、
for (int ii = 0 ; ii < n ; ++ii) {
. . .
if (method == 0)
ts[ii] = . . . . ;
else
ss[ii] = . . . ;
. . .
}
次のように変更します。
if (method == 0)
for (int ii = 0; ii < n ; ++ii) {
. . .
ts[ii] = . . . ;
. . .
}
else
for (int ii = 0 ; ii < n; ++ii) {
. . .
ss[ii] = . . . ;
. . .
}
上記の 2 つの手法は、MPAS-Oi 海洋コードに適用されたものです。MPAS-O コードは、地球の海洋システムをシミュレートして、数か月から数千年のタイムスケールで表示します。このコードは、1km 未満の地域および大循環を扱います。LANL の Douglas Jacobsen 氏ii が参加して行われた ParaTools との共同作業では、TAU Performance System* を使用して、インテル® Xeon Phi™ コプロセッサーにおけるこのルーチンのベクトル強度を測定しました。コンパイラー・レポートに基づいて、ベクトル強度が低いデータのコードとレポートの内容を調べました。
コードの一部を次に示します。
do k=3,maxLevelCell(iCell)-1
if(vert4thOrder) then
high_order_vert_flux(k, iCell) = &
mpas_tracer_advection_vflux4( tracer_cur(k-2,iCell),tracer_cur(k-1,iCell), &
tracer_cur(k,iCell),tracer_cur(k+1,iCell), w(k,iCell))
else if(vert3rdOrder) then
high_order_vert_flux(k, iCell) = &
mpas_tracer_advection_vflux3( tracer_cur(k-2,iCell),tracer_cur(k-1,iCell), &
tracer_cur(k,iCell),tracer_cur(k+1,iCell), w(k,iCell), coef_3rd_order )
else if (vert2ndOrder) then
verticalWeightK = verticalCellSize(k-1, iCell) / (verticalCellSize(k, iCell) +&
verticalCellSize(k-1, iCell))
verticalWeightKm1 = verticalCellSize(k, iCell) / (verticalCellSize(k, iCell) +&
verticalCellSize(k-1, iCell))
high_order_vert_flux(k,iCell) = w(k,iCell) * (verticalWeightK * tracer_cur(k,iCell) +&
verticalWeightKm1 * tracer_cur(k-1,iCell))
end if
tracer_max(k,iCell) = max(tracer_cur(k-1,iCell),tracer_cur(k,iCell),tracer_cur(k+1,iCell))
tracer_min(k,iCell) = min(tracer_cur(k-1,iCell),tracer_cur(k,iCell),tracer_cur(k+1,iCell))
end do
このコードの do ループ内には、サブルーチン呼び出しと不変条件の両方が含まれていたため、サブルーチンをベクトル化可能にして、ループと条件の位置を変更しました。新しいコードは次のようになります。
! Example flipped loop
if ( vert4thOrder ) then
do k = 3, maxLevelCell(iCell) - 1
high_order_vert_flux(k, iCell) = &
mpas_tracer_advection_vflux4( tracer_cur(k-2,iCell),tracer_cur(k-1,iCell), &
tracer_cur(k,iCell),tracer_cur(k+1,iCell), w(k,iCell))
end do
else if ( vert3rdOrder ) then
do k = 3, maxLevelCell(iCell) - 1
high_order_vert_flux(k, iCell) = &
mpas_tracer_advection_vflux3( tracer_cur(k-2,iCell),tracer_cur(k-1,iCell), &
tracer_cur(k,iCell),tracer_cur(k+1,iCell), w(k,iCell), coef_3rd_order )
end do
else if ( vert2ndOrder ) then
do k = 3, maxLevelCell(iCell) - 1
verticalWeightK = verticalCellSize(k-1, iCell) / (verticalCellSize(k, iCell) +&
verticalCellSize(k-1, iCell))
verticalWeightKm1 = verticalCellSize(k, iCell) / (verticalCellSize(k, iCell) +&
verticalCellSize(k-1, iCell))
high_order_vert_flux(k,iCell) = w(k,iCell) * (verticalWeightK * tracer_cur(k,iCell) +&
verticalWeightKm1 * tracer_cur(k-1,iCell))
end do
end if
このケースでは、この記事で紹介した手法の 2 つ (関数/サブルーチンを SIMD 対応にする/ベクトル化可能にする、不変条件の位置を変更する) を組み合わせて、コードをベクトル化し、パフォーマンスを向上しました。通常、コードをチューニングするには、複数の手法を適用する必要があります。変更はそれぞれ、正しい方向へ向かう 1 つのステップにすぎません。場合によっては、データレイアウトの変更、プラグマやディレクティブの追加、データのアライメントなど、すべての変更が行われるまでパフォーマンスが向上しないこともあります。各要素は、パフォーマンスを向上する 1 つのステップです。ほかの手法については、この後のセクションで説明します。
一時スカラーのショートアレイへの展開
一時的な値は通常、for または do ループの中で計算されます。この処理は、中間値をいくつかの計算で使用するために行われます。計算の共通のサブセットは、計算後、再利用するためにしばらく保持されます。また、コードを読みやすくする目的で行われることもあります。この状況で「SIMD を考慮する」を適用した場合、一時配列を、コードを実行する最も広い SIMD レジスターと同じ長さのショートベクトルにすることを意味します。
この手法は、心臓細胞のカルシウム動態に関する偏微分方程式系を解く有限要素法および有限体積法に適用されました。カルシウムイオンは、心臓の鼓動を規則的に繰り返す重要な役割を果たしています。カルシウムは、カルシウム放出ユニット (CRU) として知られる、細胞の個別の位置の格子で心臓細胞に放出されます。カルシウムが CRU から放出される確率は、その CRU のカルシウム濃度に依存します。CRU がカルシウムを放出すると、カルシウム依存の局所濃度は急激に増加し、拡散するカルシウムが隣接するサイトで放出される可能性が高くなります。CRU のシーケンスが細胞でカルシウムの放出を開始するとともに、放出は濃度上昇のウェーブに自己組織化されます。生理学的シグナリング (例えば、心筋活動電位) の引き金となるウェーブは、不整脈や生死にかかわる心室細動を引き起こすことがあります。これらの動態は、Leighton T. Izu 氏により開発された、3 つの時間依存の偏微分方程式系によりシミュレートされます。
Matthias K. Gobbert 氏および協力者により開発された、これらのカルシウム動態をシミュレートする特殊目的の MPI コードについて考えてみましょう (www.umbc.edu/~gobbert/calcium (英語))。このコードは、有限要素法または有限体積法および matrix-free リニアソルバーを使用して偏微分方程式系を解いています。TAU Performance System* のようなプロファイラーを使用すると、実行時間のほとんどが行列ベクトル乗算関数で費やされていることが分かりました。
この関数の代表的なコードiii を次に示します。
for(iy = 0; iy < Ny; iy++) {
for(ix = 0; ix < Nx; ix++) {
iz = l_iz + spde.vNz_cum[id];
i = ix + (iy * Nx) + (iz * ng);
l_i = ix + (iy * Nx) + (l_iz * ng);
t</em></strong> = 0.0;
if (ix == 0) {
t -= ( 8.0/3.0 * Dxdx) * l_x[l_i+1 ];
diag_x = 8.0/3.0 * Dxdx;
} else if (ix == 1) {
t -= ( bdx + 4.0/3.0 * Dxdx) * l_x[l_i-1 ];
t -= ( Dxdx) * l_x[l_i+1 ];
diag_x = bdx + 7.0/3.0 * Dxdx;
}
if (iy == 0) {
. . .
} else if (iy == 1) {
t -= (bdy + 4.0/3.0 * Dydy) * l_x[l_i-Nx];
t -= (Dydy) * l_x[l_i+Nx];
diag_y = bdy + 7.0/3.0 * Dydy;
} else if (iy == Ny-2) {
t -= (bdy + Dydy) * l_x[l_i-Nx];
t -= 4.0/3.0 * Dydy * l_x[l_i+Nx];
diag_y = bdy + 7.0/3.0 * Dydy;
} else if (iy == Ny-1) {
t -= (2*bdy + 8.0/3.0 * Dydy) * l_x[l_i-Nx];
diag_y = 2*bdy + 8.0/3.0 * Dydy;
} else {
t -= (bdy + Dydy) * l_x[l_i-Nx];
t -= Dydy * l_x[l_i+Nx];
diag_y = bdy + 2.0 * Dydy;
}
if (iz == 0) {
.
.
.
}
.
.
.
if (il == 1) {
.
.
.
l_y[l_i] += t*dt + (d + dt*(diag_x+diag_y+diag_z + a +
getreact_3d (is,js,ns, l_uold, l_i) )) * l_x[l_i];
} else {
l_y[l_i] += t*dt + (d + dt*(diag_x+diag_y+diag_z + a )) *
l_x[l_i];
}
}
}
一時変数 t は、ショートアレイ t>emp[8] になるように拡張されます。さらに、getreact_3d() の関数呼び出しと等価な値を格納する新しいショートベクトル alocal が作成されます。プログラミングを簡単にするため、インテル® Cilk™ Plus 表現が使用されています。一時配列が使用されると、新しいコードは次のようになります。
for(iy = 0; iy < Ny; iy++) {
...
for(ix = 8; ix < Nx-9; ix+=8) {
i = ix + (iy * Nx) + (iz * ng);
l_i = ix + (iy * Nx) + (l_iz * ng);
temp[0:8] = 0.0;
temp[0:8] -= ( bdx + Dxdx) * l_x[l_i-1:8 ];
temp[0:8] -= ( Dxdx) * l_x[l_i+1:8 ];
diag_x = bdx + 2.0 * Dxdx;
if (iy == 0) {
temp[0:8] -= ( 8.0/3.0 * Dydy) * l_x[l_i+Nx:8];
diag_y = 8.0/3.0 * Dydy;
} else if (iy == 1) {
temp[0:8] -= ( bdy + 4.0/3.0 * Dydy) * l_x[l_i-Nx:8];
temp[0:8] -= ( Dydy) * l_x[l_i+Nx:8];
diag_y = bdy + 7.0/3.0 * Dydy;
} else if (iy == Ny-2) {
temp[0:8] -= (bdy + Dydy) * l_x[l_i-Nx:8];
temp[0:8] -= 4.0/3.0 * Dydy * l_x[l_i+Nx:8];
diag_y = bdy + 7.0/3.0 * Dydy;
} else if (iy == Ny-1) {
temp[0:8] -= (2*bdy + 8.0/3.0 * Dydy) * l_x[l_i-Nx:8];
diag_y = 2*bdy + 8.0/3.0 * Dydy;
} else {
temp[0:8] -= (bdy + Dydy) * l_x[l_i-Nx:8];
temp[0:8] -= Dydy * l_x[l_i+Nx:8];
diag_y = bdy + 2.0 * Dydy;
}
if (iz == 0) {
.
.
.
}
.
.
.
if (il == 1) {
. . .
alocals[0:8] = . . .
// getreact_3d() 関数で行われる演算
l_y[l_i:8] += temp[0:8]*dt + (d + dt*(diag_x+diag_y+diag_z + a +
alocals[0:8])) * l_x[l_i:8];
} else {
l_y[l_i:8] += temp[0:8]*dt + (d + dt*(diag_x+diag_y+diag_z + a )) *
l_x[l_i:8];
}
. . .
}
}
これらの変更をコードに適用することで、インテル® Xeon Phi™ コプロセッサー 5110P における実行時間は 68 時間 45 分から 38 時間 10 分に (約 44 パーセント) 短縮されました。
データ・アライメント
オリジナルのループは ix = 0 から Nx – 1 までです。ix = 0 または 1 をカバーするため、いくつかの特別な条件がありましたが、新しいコードでは、ix = 2 から Nx – 1 の代わりに、8 からループを開始しています。この処理は、カーネルループのデータ・アライメントを保つために行われたものです。
フル SIMD レジスター幅での操作に加えて、SIMD レジスターへ移動するデータがキャッシュライン境界でアライメントされていると、パフォーマンスは向上します。これは特に、インテル® Xeon Phi™ コプロセッサーで顕著です (すべてのプロセッサーに当てはまりますが、パフォーマンスに与える影響はインテル® Xeon Phi™ コプロセッサーで最も大きくなります)。配列は、最初にキャッシュ境界でアライメントされます。ix ループに入る前に ix=0,7 が処理されると、ix ループ内の動作はすべて、(キャッシュライン境界にアライメントされる) 配列のサブセクションで行われます。この場合、ソフトウェア開発者が assume aligned プラグマを追加していれば良かったでしょう。コードのパフォーマンスは向上しませんが、アライメントされたカーネルループを開始する前に実行するピールループをコンパイラーが追加する必要がなくなるためです。以前の記事で、私は、アライメントされていない行列が選択されたカーネルのパフォーマンスを 53 パーセント以上低下させる可能性を指摘しました。インテル® Xeon® プロセッサー E5-2620 ベースのプラットフォームで、単純な行列乗算テスト (アライメントあり行列およびアライメントなし行列) を行った結果を表 1 に示します。
| バージョン | 時間 (秒) |
| アライメントあり | 3.78 |
| アライメントなし | 4.86 |
表 1: 行列乗算テストの結果 – アライメントありとアライメントなし
コードセグメントは、https://github.com/drmackay/samplematrixcode (英語) から入手できます。
データレイアウト
データがアクセスされる方法でデータレイアウトが構成されると、ソフトウェアのパフォーマンスは向上します。以下の例は、ParaTools の ThreadSpotteriv のチュートリアル・コードを使用しています (ケースのビルドおよび実行に ThreadSpotter は必要ありません)。最初のケースでは、データベースのフィルおよびアクセスにリンクリストを使用していました。初期データ格納要素は、次のように定義された構造体でした。
struct car_t {
void randomize();
color_t color;
model_t model;
std::string regnr;
double weight;
double hp;
};
これらの構造体からリンクリストが作成された後、クエリーが行われます。リンクリストは、プロセッサーのプリフェッチ・セクションにとって正確な予測が困難な、ランダムで予測不能な方法でデータにアクセスします。表 2 では、「リンクリスト」行として示されています。リンクリストが標準 C++ ベクトルクラスで置換されると、データは線形でアクセスされます。
ベクトルコードを次に示します。
class database_2_vector_t : public single_question_database_t
{
public:
virtual void add_one(const car_t &c);
virtual void finalize_adding();
virtual void ask_one_question(query_t &query) const;
private:
typedef std::vector<car_t> cars_t;
cars_t cars;
};
表 2 では、「ベクトル」行として示されています。表 2 で示されているように、この変更されたアクセスパターンを利用すると、パフォーマンスは大幅に向上します。この変更は、同じ構造体を保存します。クエリーが車の色に関連している場合、構造体全体がキャッシュに書き込まれますが、使用されるのは構造体の 1 つの要素 (color) のみです。この場合、メモリーバスがメモリーとキャッシュ間の余分なデータ転送で占有され、余分な帯域幅とキャッシュリソースの両方が消費されます。
次のケースでは、前の 2 つの例で使用されていた cars 構造体を、新しいクラスに変更しています。
class database_3_hot_cold_vector_t : public single_question_database_t
{
public:
virtual void add_one(const car_t &c);
virtual void finalize_adding();
virtual void ask_one_question(query_t &query) const;
private:
typedef std::vector<color_t> colors_t;
typedef std::vector<model_t> models_t;
typedef std::vector<double> weights_t;
colors_t colors;
models_t models;
weights_t weights;
typedef std::vector<car_t> cars_t;
cars_t cars;
};
colors_t、models_t、weights に別のベクトルが用意されていることに注意してください。クエリーが色に基づいている場合、colors_t ベクトルのみキャッシュに書き込まれ、モデルと重さ情報はキャッシュに書き込まれないため、データ帯域幅および L1 キャッシュ使用の負荷が減ります。検索のためキャッシュに書き込まれたベクトルは「ホット」、キャッシュに書き込まれなかったベクトルは「コールド」と呼ばれます。表 2 では、「ホット-コールドベクトル」行として示されています。この手法では、データは適切なユニットストライド方式でアクセスされ、SIMD レジスターのすべてのレーンを使用します。表 2 のパフォーマンスの向上を確認してください。
この最後のデータレイアウトの変更は、構造体配列 (AOS) から配列構造体 (SOA) への変更に相当します。AOS から SOA への変更のコンセプトは、データがアクセスされる方法で、データを連続して配置することです。AOS で操作するよりも SOA を採用するほうが有利な場合など、AOS から SOA への変更について、さらに調査することを推奨します。
| バージョン | 平均時間/クエリーセット | スピードアップ |
| リンクリスト | 11.1 | 1 |
| ベクトル | 0.32 | 34 |
| ホット-コールドベクトル | 0.22 | 50 |
表 2: データレイアウトがインテル® Xeon® プロセッサー E5-2620 ベースのプラットフォームのパフォーマンスに与える影響
まとめ
現在のプラットフォームで利用可能なベクトルレジスターをソフトウェアで効率的に利用すると、パフォーマンスは大幅に向上します。この記事では、次の手順を説明しました。
- 適切なプラグマとディレクティブを使用する
- SIMD 対応のユーザー定義関数/サブルーチンを利用する
- 最内ループの外側へ不変条件を移動する
- 使用される順にデータを格納する
- キャッシュライン境界にデータをアライメントする
これらの手法を採用し、コンパイラー最適化レポートの情報を利用するソフトウェア開発者は、ソフトウェアのパフォーマンスを向上することができるでしょう。インテル® Advisor のようなツールは、ベクトル化の向上にも役立ちます。ベクトル化は、ソフトウェアの最適化およびパフォーマンスの最適化の重要なステップです。これらの手法の採用についての詳細は、インテル® デベロッパー・ゾーンの Modern Code サイト (https://software.intel.com/en-us/modern-code) を参照してください。
i MPAS-O 海洋コードの開発は、DOE Office of Science BER (アメリカ合衆国エネルギー省/科学部/生物学・環境研究) のサポートを受けていました。
ii Douglas Jacobsen 氏の研究は、DOE Office of Science BER (アメリカ合衆国エネルギー省/科学部/生物学・環境研究) のサポートを受けていました。MPAS コード例は使用許諾を受けて使用しています。
iii Samuel Khuvis、「Porting and Tuning Numerical Kernels in Real-World Applications to Many-Core Intel Xeon Phi Accelerators」、博士論文、数学統計学科、メリーランド大学バルティモア・カウンティー校、2016 年 5 月。コードセグメントは使用許諾を受けて使用しています。
iv ThreadSpotter は ParaTools, Inc. により配布されています。チュートリアル・コードは使用許諾を受けて使用しています。インテル® Advisor は、インテル® Parallel Studio XE の一部としてインストールされます。
コンパイラーの最適化に関する詳細は、最適化に関する注意事項を参照してください。

