ゲーム・アプリケーションにおけるニューラル・ネットワーク入門

この記事は、インテル® デベロッパー・ゾーンに公開されている「An Introduction to Neural Networks With an Application to Games」の日本語参考訳です。

この記事の PDF 版はこちらからご利用になれます。

英語のオリジナルの記事は、VentureBeat で「An introduction to neural networks with an application to games」として公開されています。インテルのゲーム開発のニュースと関連トピックは、VentureBeat (英語) を参照してください。

はじめに

音声認識、手書き文字認識、顔認識: コンピューター・プログラムは通常、人間よりもはるかに高速にタスクを処理できますが、人間には簡単に解くことができるにもかかわらず、コンピューター・プログラムには非常に難易度の高いタスクもあります。それらのタスクの一部は、現時点で最も洗練されたコンピューター・プログラムを利用しても完全に解くことはできません。では、「コンピューターと人間の違い」はどこにあるのでしょうか。

ここでは、この質問のすべてに答えることはありませんが、その中の 1 つについて簡単に見ていきます。結論から述べると、人間の脳の生物学的構造は、これらの問題を素早く解くように訓練された、単純な計算ユニットの大規模な並列ネットワークで構成されているということです。このネットワークをコンピューター上でシミュレーションしたものを、ニューラル・ネットワークまたは人工ニューラル・ネットワークと呼びます。

図 1 は、その概念を調査するために利用した単純なゲームのスクリーンショットです。アイデアは単純で、パドルを手にした 2 人のプレイヤーと、プレイヤー間を前後に移動するボールがあります。各プレイヤーは、ボールを相手に打ち返せる位置にパドルを移動します。ここでは、パドルの移動の制御にニューラル・ネットワークを使用し、ゲームが上達するように (パドルを正確に操作できるように) ニューラル・ネットワークを訓練しました (後述します)。

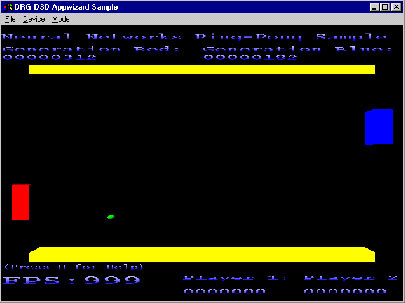
図 1: 実験用の単純なピンポンゲーム

この記事では、ニューラル・ネットワークの広大な分野に含まれる 1 つの理論である、誤差逆伝播法 (バックプロパゲーション) について説明します。次に、ピンポンゲームの基本と実装について説明します。最後に、ニューラル・ネットワークを利用することにより難問を解決できるいくつかの分野を紹介します。まず、ニューロンが人間の脳でどのように動作しているか単純化して見ることから始めます。

ニューラル・ネットワークの基本

脳のニューロン
20 世紀の初めに、スペインの解剖学者である Ramón y Cajál (ラモン・イ・カハール) は、人間の脳の働きをもたらす要素としてニューロン説を提唱しました。その後、ほかの研究者により、図 2 のように、ほかのニューロンに出力する軸索や、ほかのニューロンからの入力を受ける樹状突起の詳細が解明されました。

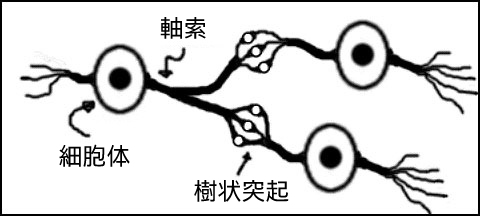
図 2: 実際のニューロンを単純化した表現

単純化して表現すると、ニューロンは多くの入力を機能的に受け取り、それらの入力を組み合わせて小さな電圧パルスの興奮性または抑制性出力を生成します。次に、その出力は軸索からほかのニューロンの (数万の) 入力に信号として伝えられます。人間の脳には約 100 億のニューロンと約 60 兆のシナプスがあることを考えれば、複雑なプロセスを実行できることは何ら不思議ではありません。神経系では、大量の並列処理を行うことにより、処理要素 (ニューロン) の速度の遅さ (ミリ秒) を補っています。

この記事の残りの部分では、紹介したモデルに基づいた人工ニューロンを使用して、人間やほかの動物の一般的な動作を模倣する方法を説明します。100 億のニューロンと 60 兆のシナプスをシミュレートすることはできませんが、単純なライバルを追加してゲームを面白くすることはできます。

人工ニューロン

20 世紀中頃の研究者たちは、いま紹介した単純なモデルを使用して、脳のニューロンの働きをシミュレートする数学的モデルを導き出しました。研究者たちは、実際のニューロンのいくつかの様相を無視して、分かりやすいモデルを考えることにしました。図 3 では、ニューロンは、入力 (X₀、X₁…X_n) と重み (W₀、W₁…W_n) を受け取り、それらの積を合計し、膜電位 v を生成して活性化関数 φ(v) に渡し、最終的な出力 y を生成する計算ブロックとして描かれています。

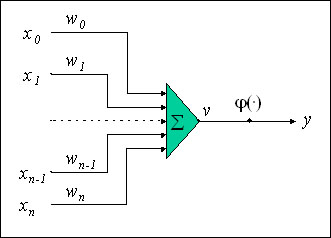
図 3: ニューロンの数学的モデル

数学の式にすると、次のようになります。

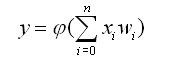
このモデルの要素を説明する際に使用した 2 つの新しい用語、膜電位と活性化関数とは何かを見ていきましょう。図で示されているように、ニューロンの膜電位は合計ユニットの出力です。入力と重みの値の範囲が -w から +w である場合、膜電位の範囲も同じです。単に膜電位がほかのニューロンに伝えられるのであれば、ニューラル・ネットワークは、単純で、直線的な計算を行うだけです。そこで、より複雑な計算を可能にするため、活性化関数が考案されました。1943 年に、McCulloch (マカロック) と Pitts (ピッツ) は 1 つの最も単純な活性化関数を考案しました。この関数は、膜電位が 0 以上の場合は 1 を出力し、その他の場合は 0 を出力する、単なる閾値関数です。一部の単純な問題はマカロック-ピッツのモデルを使用して解くことができますが、より複雑な問題には、より複雑な活性化関数が必要です。現在、最も広く利用されている活性化関数の 1 つにシグモイド関数があります。この関数は次のように表されます。

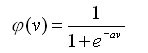
シグモイド関数には、活性化関数として使用するのに適した 2 つの重要な性質があります。

(閾値関数と異なり) どこでも微分可能です。後で述べるように、簡単な方法でネットワークを訓練することができます。
出力は非線形と線形両方の範囲を含みます。

双曲線正接 φ(v)=tanh(v) のようなほかの活性化関数も同様に使用されます。この記事の例では、特に明記している場合を除いてシグモイド活性化関数を使用しています。

ニューロンの接続

人工ニューロンの数学的モデルを示すことにより、ニューラル・ネットワークの基本的な構成要素を説明しました。いくつかの比較的単純な問題は単一ニューロンを使用して解くことができますが、より複雑な問題ではニューロンのネットワーク、つまりニューラル・ネットワークを使用する必要があります。

ニューラル・ネットワークは、複数の層で接続された複数のニューロンからなります。ほとんどのネットワークでは、どんな方法でも互いに接続されないニューロン層が含まれています。ネットワーク層の間の相互接続パターンは規則的でも、さまざまなニューロン間のリンクに関連付けられている重みは大幅に異なることがあります。図 4 は、最初の層に 2 つのノード、2 番目の層に 3 つのノード、3 番目の層に 1 つのノードがある、3 層のネットワークを示しています。最初の層のノードは入力ノード、3 番目の層のノードは出力ノード、入力層と出力層の間の層のノードは隠れノードと呼ばれます。

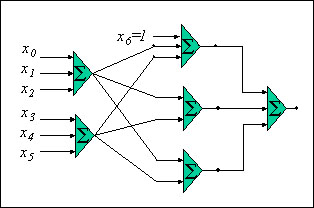
図 4: 3 層のニューラル・ネットワーク

隠れ層の最初のノードの入力が x₆ になっていることに注目してください。この固定入力 (x₆) はほかのニューロンから伝えられたものではありませんが、定数値のラベルが付けられています。これはバイアスと呼ばれ、ニューロンの発火を調整するために使用されます。バイアスには関連付けられている重み (図には表示されていません) がありますが、入力値は変わりません。すべてのニューロンは、その入力の 1 つを定数値にして固定することにより、バイアスを追加することができます。この記事ではネットワークの訓練はまだ説明していませんが、その説明の際に、ほかの入力の重みのように、バイアスに影響する重みを訓練できることが分かるでしょう。

この記事で扱うニューラル・ネットワークは、図 4 と構造的に似ています。この種のネットワークの主な特徴は次のとおりです。

ネットワークは複数の層からなります。1 つの入力層、1 つの出力層、および 0 以上の隠れ層があります。
ネットワークは循環しません。つまり、ノードの出力は、同じ層または前の層ではなく、次の層の入力に伝えられます。
図 4 のネットワークは完全に接続されていますが、1 つの層のすべてのニューロンが次の層のすべてのニューロンに出力する必要はありません。

ニューラル・ネットワークを使用した計算

ニューラル・ネットワークの構造を簡単に説明しました。では次に、ニューラル・ネットワークを使用してどのように計算を行うことができるかを見ていきましょう。重みを調整またはネットワークを訓練して目的の計算を行う方法については、次のセクションで説明します。

最も単純なレベルでは、単一ニューロンは指定された入力のセットについて 1 つの出力を生成し、出力はその入力のセットで常に同じです。数学では、これを函数や写像と言います。このニューロンでは、入力と出力の正確な関係は、入力に影響する重みおよびニューロンで使用される特定の活性化関数により与えられます。

ニューラル・ネットワークの計算能力を示すために、一般的に使用される単純な例を見ていきましょう。この例では、使用する活性化関数はマカロック-ピッツの閾値関数であると仮定しています。ニューラル・ネットワークを使用して AND 論理ゲートの真理値表を計算する方法を調べます。AND ゲートの出力は、両方の入力が 0 の場合は 1、その他の場合は 0 になることを思い出してください。図 5 は、AND 演算子の真理値表です。

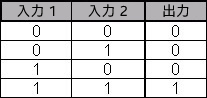
図 5: AND 演算子の真理値表

2 つの入力と 1 つの出力のニューラル・ネットワークを構築し、図 5 の真理値表を計算します。

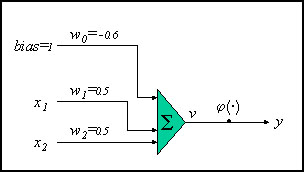
図 6: AND 関数計算のニューラル・ネットワーク

図 6 は、目的の計算を行うことが可能なニューロンの構成を示しています。前述したように、使用する活性化関数はマカロック-ピッツの閾値関数です。バイアスの重み (w₀) は -0.6 です。これは、X₁ と X₂ の両方が 0 の場合、膜電位 v は -0.6 になる、つまり出力は 0 になることを意味します。X₁ または X₂ のいずれかが 1 の場合、膜電位は 0.5+(-0.6)= -0.1 になり、まだ負であるため、活性化関数の出力は 0 になります。両方の入力が 1 の場合のみ、膜電位は負でなくなり (0.4)、活性化関数の出力は 1 になります。

この程度の問題にニューラル・ネットワークを使用する必要はありませんが、これはあくまでも単一ニューロンの計算能力に関する重要なポイントを示す開始点にすぎません。この問題と別の問題を調べることにより、線形に分離可能な問題の概念を理解します。

図 7 のグラフを見てください。ここで、x 軸は入力 0 に対応し、y 軸は入力 1 に対応しています。出力はグラフに書かれていて、図 5 の真理値表に対応しています。グレイの領域は、(入力が 0 から 1 の実線に沿って有効であると仮定した場合に) 出力が 1 になる範囲を表しています。

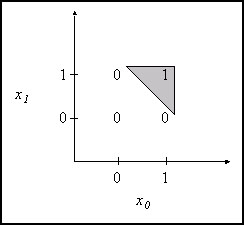
図 7: AND 関数のグラフ

注目すべき点は、出力が 1 になる入力値と出力が 0 になる入力値を分離する線 (グレイ領域の斜めの線) があることです。そのような「境界線」を引くことができる問題 (AND 問題など) は、線形に分離可能な問題として分類されます。

次に、別の論理演算子の場合を見てみましょう。図 8 は、排他的論理和 (XOR) 演算子の真理値表です。

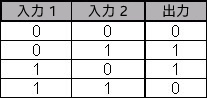
図 8: XOR 演算子の真理値表

XOR の出力は、いずれかの入力が 1 の場合のみ 1 になります。この演算子の「グラフ」を図 9 に示します。

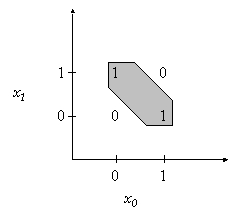
図 9: XOR 関数のグラフ

出力 1 のグレイの領域は、1 つの線ではなく 2 つの線 (グレイ領域の上と下の斜線) で分離されています。この問題は線形に分離可能ではありません。この函数を計算できる単一ニューロンを構成しようとしても成功しません。

黎明期の研究者たちは、これが人工ニューロンを使用したすべての計算の制限であると考えました。多層の追加が行われた場合にのみ、動作が線形のニューロンを組み合わせて線形に分離できない問題を解くことが可能であると考えられました。図 10 は、XOR 問題を解くことができる、単純な、3 つのニューロンのネットワークです。ここでも、使用する活性化関数はマカロック-ピッツの閾値関数であると仮定しています。

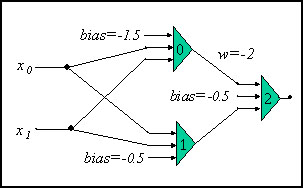
図 10: XOR 関数計算のニューラル・ネットワーク

w=-2 の重みを除いて、重みはすべて 1.0 で固定です。完璧を期すため、4 つの異なる入力の組み合わせの出力をすべて見ていきましょう。

両方の入力が 0 の場合、ニューロン 0 と 1 はどちらも 0 を出力します (バイアスがどちらも負であるため)。そのため、ニューロン 2 の出力も 0 になります (バイアスが負で両方の入力が 0 であるため)。
X₀ が 1 で X₁ が 0 の場合、ニューロン 0 は 0 を出力し、ニューロン 1 は 1 を出力して (1.0+(-0.5)=0.5 は 0 より大きいため)、ニューロン 2 も 1 を出力します。
X₀ が 0 で X₁ が 1 の場合、ニューロン 0 は 0 を出力し、ニューロン 1 は 1 を出力して、ニューロン 2 は 1 を出力します。
最後に、両方の入力が 1 の場合、ニューロン 0 は 1 を出力し、ニューロン 2 の入力は -2 になります (重みが負のため)。ニューロン 1 は 1 を出力し、入力 -2 とバイアス -0.5 の組み合わせにより、ニューロン 2 の出力は 0 になります。

この単純な例から分かるのは、非線形の分離可能な問題を解くためには多層ネットワークが必要であるということです。また、この問題はマカロック-ピッツの閾値関数で簡単に解くことができますが、現実的な問題を解くには、より数学的に扱いやすい (例えば、微分可能な) 活性化関数が必要です。では、ニューラル・ネットワークを (プログラムや構造化するのではなく) 訓練して特定の問題を解く方法を説明しましょう。

学習プロセス

単一ニューロンの出力の定義に戻りましょう (特定のデータセットのパラメーター k を追加しました)。

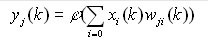
式 1

ニューロン j が入力ニューロンでない場合、x = y (ニューロン i の出力) になります。また、w は、ニューロン j の入力としてニューロン i の出力に接続される重みです。

出力 y(k) が想定した結果にならない場合や指定された入力のセット x(k) が必要ない場合に、さまざまな重み w(k) の値を変更する方法を決めます。形式的に、d(k) を指定された入力のセット k の目的の出力とします。次に、誤差関数 e(k)=d(k)-y(k) を見ます。誤差が少なくなるように (理想的には 0 になるように) 重みを調整します。誤差エネルギーを誤差の関数として見ます。

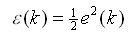
式 2

重みを調整することは、?(k) を最小化することになります。さまざまな重み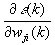について誤差エネルギーの勾配を見ます。

式 1 と式 2 を組み合わせ、連鎖律を使用して (y(k)=?(v(k)) および v(k)=?w(n)y(n) であることを思い出して)、この導関数を扱いやすくします。

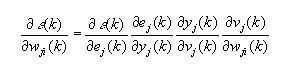
式 3

式 3 の各項を整理すると、次のようになります。

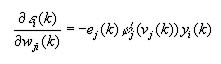
式 4

ここで、?'() は引数の微分を表します。重みの調整は、デルタルールを使用して記述できます。

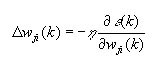
式 5

ここで、η は学習率パラメーター (値は 0 から 1) です。このパラメーターは、重みが「勾配の上」に移動する割合を決定します。η が 0 の場合、学習は行われません。式 5 を変更して局所勾配 ?(k) を含めます。

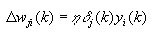
式 6

ここで、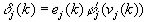 式 6 を使用して、ニューラル・ネットワークの出力層のニューロンの重みを直接更新できます。ネットワークの隠れ層と入力層のニューロンの計算は少し複雑です。これらのニューロンの重みの変更の計算には、誤差逆伝播法と呼ばれる式を使用します。微分の詳細は説明しませんが、局所勾配の式は次のようになります。

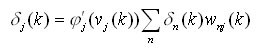
式 7

この式で、w(k) は、ニューロン n の入力としてニューロン j の出力に接続される重みを表します。このニューロンの局所勾配 ?_j を計算できれば、式 6 を使用して重みの変更を計算できます。

ネットワークのすべてのニューロンの重みの変更を計算するには、出力層から始めます。式 6 を使用して、ネットワークの出力層のすべてのニューロンの重みの変更を最初に計算します。次に、式 6 と式 7 を使用して、出力層に近い隠れ層の重みの変更を計算します。ネットワークのすべてのニューロンの重みの変更が計算されるまで、出力側から入力側へ、および左から右へ、ほかの隠れ層についてもこれらの式を使用します。最後に、ネットワークの出力を再計算して目的の結果に近くなったかどうか確認できるポイントで、重みの変更を適用します。

ネットワークの訓練は、いくつかの異なる方法で行うことができます。

重みの変更は、いくつかの入力パターンについて集計され、すべての入力パターンがネットワークに示された後に適用できます。
各入力パターンが示された後、重みの変更を適用できます。

方法 1 は最も一般的に使用されます。方法 2 を使用する場合、パターンはランダムな順でネットワークに示されます。一部の提示順に影響を受ける局所エネルギーが最小になったときにネットワークが「閉じ込められない」ようにすることが必要です。

サンプルプログラムを見る前に、1 種類の学習プロセス (誤り訂正学習を使用した誤差逆伝播法) のみ説明したことを注記して、このセクションを終わります。ほかの種類の学習プロセスには、メモリーベース学習、ヘブ学習、競合学習があります。これらの手法の詳細は、オリジナルの記事の最後にある引用文献を参照してください。

ニューラル・ネットワークの実装

最初に述べたゲームを見ることにしましょう。図 11 は、数世代の訓練を行った後のゲームのスクリーンショットです。

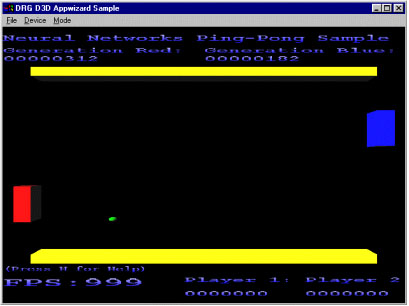
図 11: ピンポン・サンプル・アプリケーション

訓練は、中央からランダムな方向にボールを動かすことにより行われます (スピードは固定)。ニューラル・ネットワークの入力として、ボールの位置 (x,y) と方向およびパドル (ボールが向かっているパドル、赤または青) の y 位置を指定します。ネットワークは、パドルの移動先として y 方向を出力するように訓練されます。

入力層に 3 つのノード、隠れ層に 10 のノード、出力層に 1 つのノードがある、3 層のネットワークを作成しました。入力ノードにはそれぞれ、ボールの位置 (x,y) と方向およびパドルの y 位置に対応する 5 つの入力があります。これらのノードは隠れ層のノードに完全に接続され、次に出力ノードに完全に接続されます。図 12 は、入力と出力を含むネットワークのレイアウトです。重み、バイアス、活性化関数は表示されていません。

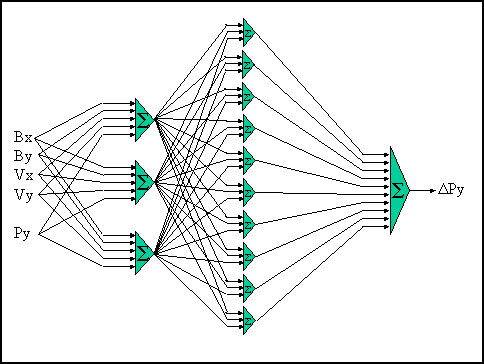
図 12: ピンポンゲームのニューラル・ネットワーク

ネットワークは、ボールの向きと同じ y 方向にパドルを移動させることを学習します。数千世代の訓練の後、ニューラル・ネットワークは完璧にプレイすることを学習します (ネットワークの重みはランダムな値に初期化されるため、世代の正確な数は異なります)。

ネットワークが予測を行わなければならないように、ボールのスピードよりもパドルのスピードを遅くして実験しました。図 12 のネットワークでいくつかの学習が行われましたが、ニューラル・ネットワークは完璧なプレイを学習することはできませんでした。ニューラル・ネットワークがこの問題を完全に学習できるようにするには、いくつかの機能をネットワークに追加する必要があります。

この例では、ニューラル・ネットワークは、コンピューターが制御する相手が持つ AI の形式にすぎません。訓練のレベルを変えることにより、コンピューターの相手のプレイは初心者から上級者まで変わります。いつ訓練を終了するか決めることは重要な課題です。1 つの簡単な解決策は、前もってネットワークを訓練する回数 (例えば 1000 回) を決めておいて、人間のプレイヤーが勝つたびに、ネットワークを追加で 100 回訓練することです。この方法では、完璧なコンピューター制御の相手を作り出すことになりますが、次第に強くなる相手も作り出すべきです。

ニューラル・ネットワークの非自明なアプリケーション

ピンポンの例はニューラル・ネットや人工知能のアプリケーションを簡単に理解できるように提供されたものであり、実社会の問題にはより多くの考慮が必要です。これからいくつかのニューラル・ネットワークの用途を簡単に説明しますが、アプリケーションに追加して問題をすべて解決できる万能のニューラル・ネットワークはないことを覚えておいてください。特定の問題の適切な解決策を見つけ出すには、ネットワークの入力および出力として使用する変数や「機能」、使用するネットワークのサイズと構成、ネットワークを訓練するために使用する訓練セットなどの情報を利用した、多くの思考や実験が必要です。

ゲームのすべての AI にニューラル・ネットワークを使用しても、前述した単純なピンポンの例よりもうまくいかないでしょう。おそらく、AI の意思決定の多くは従来の状態機械を使用して行うことになるでしょうが、決定の補完やハードコードされた状態機械の拡張にニューラル・ネットワークを利用できるかもしれません。この一例は、キャラクターの体力、利用可能な弾の数、あるいは人間の相手の体力や弾の数のような情報を入力として扱うニューラル・ネットワークです。次に、ネットワークは、実際の移動、経路探索、その他を行うために従来の AI が処理を引き継ぐポイントで、戦うか逃げるかを決定します。いくつかのゲームでは、決定の勝ち負け (あるいは体力や弾の数の増減) を調べることにより、ネットワークの意思決定プロセスを向上できるでしょう。

私が興味を持ち研究に専念した分野は、シミュレーションの実際の物理計算にニューラル・ネットワークを使用することでした。ニューラル・ネットワークの訓練とは結局のところ、いくつかのデータのセットに適した関数を見つけるプロセスであるため、この分野は有望でしょう。物理的にシミュレートされたゲームの物理的なコントローラーを作成するという課題を仮定した場合でも、ニューラル・ネットワークは解決策の 1 つになるでしょう。

さまざまな形式のパターン認識にニューラル・ネットを使用することは、認識能力の向上に役立つでしょう。説明した問題でも、ネットワークがパターン (体力や弾の数、物体に作用する力、その他) の認識に使用され、適切な処理を行います。ニューラル・ネットワークの強みは、既知のパターンのセットで訓練した後、未知のパターンが提示されたときに意味のある決定を引き出すことができる能力にあります。既存のデータから新しいデータを外挿するこの機能は、最初に挙げた、音声認識、手書き文字認識、顔認識の分野に適用できます。また、株式市場分析における傾向の発見のような、「曖昧な」分野でも役に立ちます。

まとめ

この記事では、複雑な計算を最小限にすることを心がけました。サンプルコードの説明には図を利用し、誤差逆伝播法ニューラル・ネットワークの概要を説明しました。この記事がニューラル・ネットワークの概要を理解する助けとなり、紹介した単純なサンプルコードが、皆さんのアプリケーションの意思決定のためにニューラル・ネットワークを調査する価値があるかどうか判断するのに役立つことを期待しています。いくつかの参考文献をお読みになり、ニューラル・ネットワークの特徴をよく理解することを推奨します。ニューラル・ネットワークを試して、将来のゲームタイトルにリアルさを追加し、アプリケーションの生産性を高める、斬新な方法を思い付いてください。

コンパイラーの最適化に関する詳細は、最適化に関する注意事項を参照してください。