2 つの部分空間の主角度の計算

目的

内積空間の 2 つの部分空間の相対的な位置に関する情報を得る。

解決方法

部分空間はいくつかのベクトルのスパンとして表現され、部分空間の相対的な位置は部分空間の間の主角度のセットを計算して得ることができると仮定します。角度を計算するには、次の操作を行います。

各部分空間に正規直交基底を構築して、部分空間の次元を決定します。
1. 適切なサブルーチンを呼び出して (列が複数の部分空間をスパンする) 行列のピボットで QR 因数分解を行います。
2. しきい値を使用して、部分空間の次元を決定します。
3. 正規直交基底を形成します。
1 つの部分空間の基底ベクトルと別の部分空間の基底ベクトルの内積の行列を形成する
行列の特異値分解を計算します。

ソースコード: サンプル (https://www.intel.com/content/dam/develop/external/us/en/documents/mkl-cookbook-samples-120115.zip (英語)) の ANGLES/definition/main.f ファイルを参照してください。

正規直交基底を構築して部分空間の次元を決定

… 
REAL*8 Y(LDY,K),TAU(N),WORK(3*N) 
… 
! 
! ピボットで QR 因数分解を適用 
    CALL DGEQPF(N, K, Y, LDY, JPVT, TAU, WORK, INFO) 
! DGEQPF により返された INFO を処理 
… 
! ランクを計算 
    K1=0 
    DO WHILE((K1 .LT. K) .AND. (ABS(Y(K1+1,K1+1)) .GT. THRESH)) 
        K1 = K1 + 1 
    END DO 
! 
! DORGQR を呼び出して K1 直交ベクトルを形成 
    CALL DORGQR(N, K1, K1, Y, LDY, TAU, WORK, LWORK, INFO) 
! DORGQR により返されたINFO を処理 
…

内積の行列を形成して SVD を計算

REAL*8 U(N,KU),V(N,KV),W(KU,KV),VECL(KU,KMIN) 
REAL*8 VECRT(KMIN,KV),S(KMIN),WORK(5*KU) 
… 
! W=U^t*V 形式
    CALL DGEMM(‘T’, ‘N’, KU, KV, N, 1D0, U, N, V, N, 0D0, W, KU1) 
… 
! W=U^t*V の SVD
    CALL DGESVD(‘S’, ‘S’, KU, KV, W, KU, S, VECL, KU, VECRT, KMIN, WORK, LWORK, INFO) 
! DGESVD により返された INFO を処理 
…

説明

使用するルーチン
タスク	ルーチン	説明
行列のピボットを使用した QR 因数分解	dgeqpf	ピボットで一般的な m x n 行列の QR 因数分解を計算します。
正規直交基底を形成する	dorgqr	?geqpf または ?geqp3 で形成される QR 因数分解の実直交行列 Q を生成します。
1 つの部分空間の基底ベクトルと別の部分空間の基底ベクトルの内積の行列を形成する	dgemm	一般的な行列を含む行列-行列の積を計算します。
行列の特異値分解を計算する	dgesvd	一般的な長方行列の特異値分解を計算します。

最初に、各部分空間に正規直交基底を構築して、部分空間の次元を決定します。

U をいくつかの内積線形空間のベクトルを表現する列を含む N x k 行列 (N≥k) とします。この空間の正規直交基底を構築するには、行列 U の QR 因数分解を使用します。ピボットは UP = QR として表現できます。空間の次元が l (l≤k) で、丸め誤差が発生しない場合、直交 (複素数値行列のユニタリ) N x N 行列 Q および上三角 N x k 行列 R が得られます。

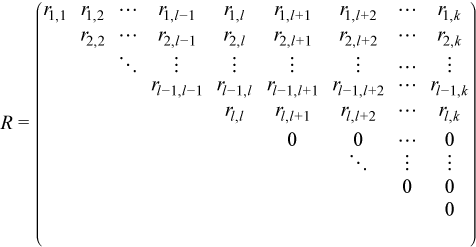
方程式 UP = QR は、U のすべての列が Q の最初の l 列の線形の組み合わせであることを意味します。ピボットにより、R の対角要素 r_j,j は絶対値の降順になります。事実、ピボットにより、より強い不等式になります。

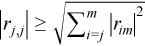
j≤m≤k。

丸め誤差を含む実際の計算では、R の右下 (k - l) x (k - l) 三角の要素は小さいがゼロではないため、しきい値 threshold を使用してランク |r_l,l| > threshold > |r_l+1,l+1| を決定します。

これで部分空間の間の角度を決定できるようになりました。

およびを、dim()=k, dim()=l、k≤l の同じ N 次元ユークリッド空間の2 つの部分空間とします。これらの部分空間の相対的な位置を見つけるには、主角度 θ₁≥θ₂≥...≥θ_k≥ 0 を使用します。次のように定義されます。

最初の角度は次のように定義されます。

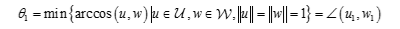
ベクトル u₁ および w₁ は主ベクトルと呼ばれます。ほかの主角度およびベクトルは再帰的に定義されます。

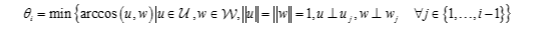
同じ部分空間の主ベクトルはペアで直交です。

(u_i, u_j) = (w_i, w_j) = δ_ij

主角度の計算には、行列の特異値分解を使用します。U および W をそれぞれサイズ N x k および N x l の行列、列をそれぞれと正規直交基底とします。k x l 行列 U^TW の SVD を計算します。

U^TW = PΣQ^T, P^TP = I_k, QQ^T = I_l

これで、Σ の対角要素が主角度の余弦であることを証明できます。

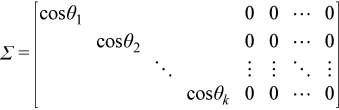
各ペアの主ベクトルは Upⁱ および Wqⁱ です。ここで、pⁱ および qⁱ は、P および Q の i 番目の列です。