フーリエ積分の評価

目的

高速フーリエ変換 (FFT) を使用して連続するフーリエ変換積分を数値的に評価する。

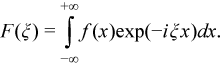
解決方法

実数値関数 f(x) が範囲 [a, b] 外のゼロで、N 個の等距離のポイント x_n = a + nT/N (ここで、T = |b - a| および n = 0, 1, ... , N-1) でサンプリングされると仮定します。FFT を使用して、ポイント ξ_k = k2π/T (ここで、k = 0, 1, ... , N/2) の積分を評価します。

インテル® oneMKL の FFT インターフェイスの使用 (C/C++)

float *f; // input: f[n] = f(a + n*T/N), n=0...N-1 
complex *F; // output: F[k] = F(2*k*PI/T), k=0...N/2 
DFTI_DESCRIPTOR_HANDLE h = NULL; 
DftiCreateDescriptor(&h,DFTI_SINGLE,DFTI_REAL,1,(MKL_LONG)N); 
DftiSetValue(h,DFTI_CONJUGATE_EVEN_STORAGE,DFTI_COMPLEX_COMPLEX); 
DftiSetValue(h,DFTI_PLACEMENT,DFTI_NOT_INPLACE); DftiCommitDescriptor(h); 
DftiComputeForward(h,f,F); 
for (int k = 0; k <= N/2; ++k) 
{ 
    F[k] *= (T/N)*complex( cos(2*PI*a*k/T), -sin(2*PI*a*k/T) ); 
}

説明

評価は積分の階段関数近似に基づき、この派生に従います。

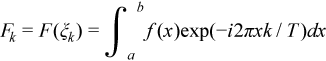
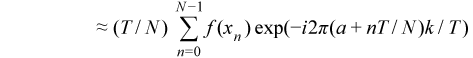
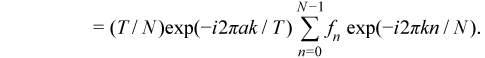
最後の行の合計は定義による FFT です。関数 f のサポートがゼロ付近で対称的に拡張される、つまり [a, b] = [-T/2, T/2] の場合、合計の前の係数は (T/N)(-1)^k になります。

関数 f が実数値の場合、F(ξ_k) = conj(F(ξ_N-k)) になります。実数から複素数 FFT の最初の N/2 + 1 複素数値は、実数入力とほぼ同じメモリーを占めます。共役により全体の結果を計算するのに十分です。FFT 計算が実数から複素数への変換を行うように構成されている場合、さらに複素数から複素数 FFT の約半分の時間がかかります。