この記事は、インテル® デベロッパー・ゾーンに掲載されている「Program Optimization through Loop Vectorization」(http://software.intel.com/en-us/articles/program-optimization-through-loop-vectorization/) の日本語参考訳です。
はじめに
この記事では、有限差分ステンシル計算を例に、インテル® メニー・インテグレーテッド・コア (インテル® MIC) アーキテクチャーのベクトルユニットの重要な利点について説明します。
for (i=0; i<dx; i++)
for (r=1; r<=2; r++)
u[i]+=c[r]*( v[i+ r*dx] + v[i- r*dx] );
この例で、dx は 2 次元配列の 1 次元側を表します。ここでは単純にするため、配列 u と v はパディングされており、[-2*dx,…,3*dx] に安全にアクセスできると仮定します。さらに一般的なケースは参考文献 (1) を参照してください。
SIMD (Single Instruction Multiple Data) 並列処理は、複数のデータセットの要素に対して同じ操作を実行する、計算負荷の高いアプリケーションのパフォーマンスを向上します。インテル® MIC アーキテクチャーの 512 ビットのベクトルユニットは、1 クロックサイクルに 16 の単精度浮動小数点値を操作することで、上記の単精度の例ではパフォーマンスが向上します。u[j:16] を 16 の単精度浮動小数点値 (u[j]、u[j+1]、...、u[j+15]) の疑似コード表現とすると、SIMD ベクトル化は次のように表すことができます。
for (i=0; i<dx; i+=16)
for (r=1; r<=2; r++)
u[i:16]+=c[r]*( v[i+r*dx:16] + v[i-r*dx:16] );
この疑似コードでは、便宜上、dx は 16 の倍数と仮定します。
ベクトル化戦略
インテル® コンパイラーでは、次の方法によりベクトル命令を生成することができます。
- インライン・アセンブリー・コード
- SIMD ベクトル組込み関数
- C++ SIMD ベクトルクラス
- OpenMP* 4.0 (SIMD 関連機能)
- インテル® Cilk™ Plus (SIMD 関連機能)
- simd プラグマ
- SIMD 対応関数
- 配列表記
- 自動ベクトル化
インライン・アセンブリーと SIMD ベクトル組込み関数を利用する場合、プログラマーは生成されるベクトルコードに対して全責任を負い、コードを完全に制御することができます。ただし、低レベルのコードを記述する必要があるため、生産性と保守性は高くありません。この記事では、高レベルのコードで最適なパフォーマンスを実現する方法に注目します。
C++ SIMD ベクトルクラスは、SIMD ベクトル組込み関数に対する C++ クラスの抽象化です。多重定義された演算子、クラスメンバー関数、フレンド関数は、プログラムの記述と保守を容易にします (通常の C/C++ コードのように利用できます)。ただし、クラス定義自体はハードウェアに依存するため、プログラマーは一度に 512 ビットのベクトルデータを操作する必要があります。
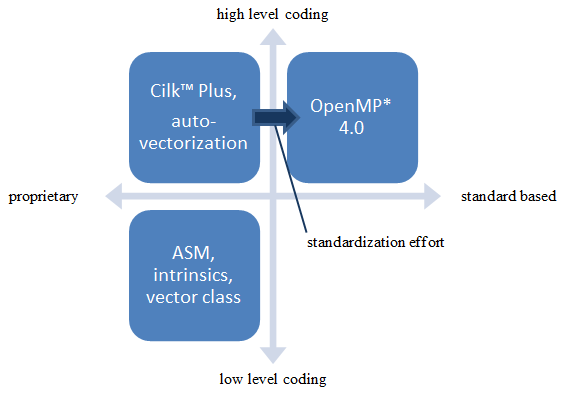
OpenMP* 4.0 (2) の SIMD ベクトルサポートは、明示的にベクトルコードを記述するための標準規格ベースの手法を提供します。この標準化の取り組みにインテルは大きく貢献しています。OpenMP* は、プログラマーにとってマルチスレッドコードを記述する一般的な手段になりました。同様に、標準ベースのベクトル・プログラミングも開発者に受け入れられることを期待しています。
インテル® Cilk™ Plus (3) 拡張は、標準化への取り組みを推進しており、その大部分が OpenMP* 4.0 で採用されました。インテルでは、ベクトル・プログラミング構造を C/C++ 言語自体に含めるように標準化委員会と協議しています。また、GCC コンパイラーと LLVM コンパイラーにも、インテル® Cilk™ Plus をサポートするように働きかけています。
インテル® コンパイラーは、最先端の自動ベクトル化テクノロジーを採用しています。ただし、アムダールの法則によると、16 ウェイのベクトル・ハードウェアでは、80% のコードをベクトル化しても (自動ベクトル化ではまれです) 4 倍のスピードアップしか得られません。例えば、コードのスカラー実行に 100 秒かかるとします。そのうち 80 秒を 16 ウェイでベクトル化可能な場合 (つまり、16 倍スピードアップできる場合)、コードの実行時間は 25 秒になります (ベクトル化されない部分に 20 秒 + ベクトル化された部分に 5 秒)。つまり、全体のスピードアップは 4 倍 (= 100/25) にしかなりません。そのため、プログラマーは自動ベクトル化だけでなく、インテル® MIC アーキテクチャーのベクトルユニットを最大限に活用することが不可欠です。
次の図は、さまざまなアプローチの関係を表しています。
データ・アライメントの最適化
インテル® MIC アーキテクチャー向けのベクトル化における最も重要な要素の 1 つは、データ・アライメントです。データが 64 バイト境界でアライメントされており、コンパイラーがアライメント情報を認識している場合、512 ビットのベクトルロード/ストアを 1 つのロード/ストア命令で実行することができます。ロードは、ベクトル加算のような命令のメモリーオペランドとして表現することもできます。コンパイラーがデータ・アライメントを認識していない場合 (通常のケース)、あるいはデータが正しくアライメントされていない場合、コンパイラーにより生成されるコードの効率が (場合によっては大きく) 低下します。そのため、データ・アライメントを最適化し、その情報をコンパイラーに適切に伝えることが重要です。
コンパイラーにベクトル化を任せる場合 (OpenMP*、インテル® Cilk™ Plus、または自動ベクトル化を利用する場合)、-vec-report6 の出力内容から、コンパイラーがアライメントされたメモリー参照を使用したか、あるいはアライメントされていないメモリー参照を使用したかが分かります。別のアプローチとして、アセンブリー・コードを解析することもできます。効率の悪いメモリーアクセスが見つかった場合、データ・アライメントを改善することで、ベクトル化コードのパフォーマンスが向上します。
次の呼び出しにより、アライメントされたヒープメモリーを割り当てることができます。
void* _mm_malloc (size_t size, size_t base)
静的に割り当てられた変数は、__declspec(align(64)) を挿入してアライメントできます。
__declspec(align(64)) float temp[SIZE]; /* ローカルの配列 temp は 64 バイト境界でアライメントされている */
等価な Fortran 宣言子は次のとおりです。
!DIR$ ATTRIBUTES ALIGN: base :: variable
__assume_aligned(pointer, base) を挿入して、ポインターが base 境界でアライメントされていることを示すことができます。
__assume_aligned(ptr, 64); /* ptr は 64 バイト境界でアライメントされている */
Fortran で A(1) のアドレスが 64 バイト境界でアライメントされていることを示すには、次の宣言子を使用します。
!DIR$ ASSUME ALIGNED A(1): 64
コンパイラーによるベクトルコードの生成
この記事の冒頭のサンプルコードをもう一度見てみましょう。
for (i=0; i<dx; i++) for (r=1; r<=2; r++) u[i]+=c[r]*( v[i+ r*dx] + v[i- r*dx] );
以下は、上記のコードと同じ計算を行う、典型的なステンシルコードです。
for (int i= 0; ix<dx; i++) {
u[i] += c1* (v[i+ dx] + v[i- dx])
+ c2* (v[i+2*dx] + v[i-2*dx]);
}
図 1: 有限差分のサンプルコード (初期バージョン)
このコードをベースとして使用します。以下は、OpenMP* 4.0 を使ってこのコードをベクトル化したバージョンです。
#pragma omp simd // OpenMP 4.0
for (int i= 0; ix<dx; i++) {
u[i] += c1* (v[i+ dx] + v[i- dx])
+ c2* (v[i+2*dx] + v[i-2*dx]);
}
以下は、インテル® Cilk™ Plus の simd プラグマを使ってこのコードをベクトル化したバージョンです。標準化への取り組みで、OpenMP* はインテル® Cilk™ Plus をモデルとしたため、この 2 つのコードはよく似ています。
#pragma simd // CilkPlus
for (int i= 0; ix<dx; i++) {
u[i] += c1* (v[i+ dx] + v[i- dx])
+ c2* (v[i+2*dx] + v[i-2*dx]);
}
インテル® Cilk™ Plus の配列表記により、次のように記述することもできます。
// 配列表記 (ロングベクトル) (long vector) u[0:dx] += c1* (v[0+ dx:dx] + v[0- dx:dx]) + c2* (v[0+2*dx:dx] + v[0-2*dx:dx]);
以下は、より明示的に 512 ビットのショートベクトル形式で記述したバージョンです。
dx1 = dx – (dx & 0xF);
for (int i= 0; ix<dx1; i+=16) {
// 配列表記 (ショートベクトル、一度に 16 要素を処理)
u[i:16] += c1* (v[i+ dx:16] + v[i- dx:16])
+ c2* (v[i+2*dx:16] + v[i-2*dx:16]);
}
for (int i= dx1; ix<dx; i++) { // リマインダー・ループ
u[i] += c1* (v[i+ dx] + v[i- dx])
+ c2* (v[i+2*dx] + v[i-2*dx]);
}
この単純なステンシルループは、自動ベクトル化することができます。また、自動ベクトル化される可能性を高める方法がいくつかあります (例えば、ベクトル化可能なソースコードを記述したり、ポインター・エイリアシングが存在しないことを示すコンパイラー・オプションを使用するなど)。これらのトピックについては、参考文献 (4) と (5) を参照してください。
コンパイラーは「バージョニング」を用いて、データ・アライメントが不明であれば実行時にアライメントをテストし、アライメントされていると仮定してより高速なバージョンのループを実行するか、あるいはアライメントされていないと仮定してより遅いバージョンを実行します。ただし、バージョニングには追加のオーバーヘッド、コードサイズ、コンパイル時間が生じます。また、多数のデータ・アライメントが不明な場合は対応できません。そのため、最適なパフォーマンスを達成するには、明示的なデータ・アライメントの最適化が不可欠です。
C++ SIMD ベクトルクラスによるコーディング
より積極的な方法は、SIMD 命令を直接使用して、ベクトル化されたループをプログラムすることです。色々な方法がありますが、最も手間がかかるのは、アセンブリー言語で直接プログラムする方法です。コンパイラーがサポートする組込み関数を利用する方法もあります。これは、SIMD を容易にコーディングし、同じソースコードでハードウェア・レベルの SIMD 命令と高水準の C/C++ 命令を組み合わせることができます (7)。ステンシルコードのように算術演算と論理演算が大半を占めるアプリケーションでは、SIMD 組込み関数の代わりにインテルの C++ SIMD クラスを利用できます。
インテルの C++ SIMD クラスは、配列 (ベクトルデータ) を並列に処理できます。整数ベクトル (Ivec) クラスと浮動小数点ベクトル (Fvec) クラスをサポートしており、インテル® MIC アーキテクチャーでは、クラスの名前は行う演算の種類に基づいています。例えば、F32vec16 は 16 のパックド 32 ビット浮動小数点データの演算を行い、F64vec8 は 8 つのパックド 64 ビット浮動小数点データの演算を行います。標準の演算子は、+、+=、-、-=、*、*=、/、/= です。
高度な演算子には、平方根、逆数、平方根の逆数があります。インテル® MIC アーキテクチャーに適したロードとストアには、64 バイト境界でアライメントされたデータが必要です。コードサンプルでは、メインループで配列 v および u のアライメントされたアドレスから SIMD 命令を発行できるように、事前ループを追加しています。図 2 は、F32vec16 クラスを使用して y 方向のループにインテル® SSE のベクトル化を実装する例を示しています。整数値 align_offset は、配列ポインターを 64 バイト境界にアライメントする事前ループから取得した配列インデックスです。つまり、vec_v と vec_u はそれぞれ、アライメントされたメモリーアドレス v+align_offset と u+align_offset のポインターです。
ここでは、配列 u と v は同じ境界でアライメントされると仮定します。vec_v の単精度配列要素を 1 つ進めることは、配列 v の単精度要素を 16 進めるのと同等です。ループの反復数 vec_loop_trip とストライド vec_dx は、オリジナルのスカラーバージョンの dx の 16 分の 1 になります。各定数係数 ci について、コンストラクター F32vec16 は ci の 16 の同じコピーを vec_ci にパックします。
#include <micvec.h>
// インテル® MIC ベクトルレジスターに係数をロード
const F32vec16 vec_c1(c1), vec_c2(c2);
// v[] のオフセットを 64 バイト境界でアライメント
const int align_offset = (64 - ((uintptr_t)v) % 64)/ sizeof(float);
// スカラー事前ループ (最初の 64 バイト境界でアライメントされていない要素)
#pragma loop count max(15)
for (int i=0; i< align_offset; i++) {
u[i] += c1* (v[i+ dx] + v[i- dx])
+ c2* (v[x+2*dx] + v[i-2*dx]);
}
// アライメントされているベクトルレジスター配列 – u と v は同じ境界でアライメントされると仮定
F32vec16* vec_v = (F32vec16*)(v+align_offset);
F32vec16* vec_u = (F32vec16*)(u+align_offset);
const int vec_loop_trip = (dx - align_offset) / 16;
const int vec_dx = dx / 16;
// ベクトルレジスターに対するループ
for(int i=0; i<vec_loop_trip; i++) {
vec_u[i] += vec_c1* (vec_v[i+ vec_dx] + vec_v[i- vec_dx])
+ vec_c2* (vec_v[i+2*vec_dx] + vec_v[i-2*vec_dx]);
}
// スカラー・リマインダー・ループ (残りの要素)
#pragma loop count max(15)
for (int i=align_offset+16*vec_loop_trip; i<dx; i++) {
u[i] += c1* (v[i+ dx] + v[i- dx])
+ c2* (v[i+2*dx] + v[i-2*dx]);
}
図 2: インテルの C++ SIMD クラスによりベクトル化されたループ。メインループの各反復は vec_v と vec_v の 16 のパックド要素の操作を行います。
これらのクラスを利用することで、インテル® アドバンスト・ベクトル・エクステンション (インテル® AVX) のような新しいハードウェア言語拡張に容易に移行することもできます (3)。データ・アライメントとレジスターごとの浮動小数点スカラーの数に C マクロ定義を用いてコードを一般化することで、インテル® MIC アーキテクチャー、インテル® AVX、インテル® ストリーミング SIMD 拡張命令 (インテル® SSE) 向けに再コンパイルできるようになります。図 3 は、マシン固有の要素数やアライメント要件などを抽象化することで、図 2 の実装をすべてのインテル® アーキテクチャー向けに拡張し、インテル® Xeon® プロセッサーとインテル® MIC アーキテクチャー間の移植を容易にします。サンプルコードで使用されている C マクロ BUILD_FOR_MIC と BUILD_FOR_AVX は、コンパイラーにより生成されるマクロ __MIC__ と __AVX__ に置換できます。
// ハードウェア・レジスター・サイズの選択
#if defined(BUILD_FOR_MIC)
# include <micvec.h>
# define FLOAT_VECTOR F32vec16
# define GOOD_ALIGN 64
# define NUM_FLOATS 16
#elif defined(BUILD_FOR_AVX)
# include <dvec.h>
# define FLOAT_VECTOR F32vec8
# define GOOD_ALIGN 32
# define NUM_FLOATS 8
#elif defined(BUILD_FOR_SSE)
# include <dvec.h>
# define FLOAT_VECTOR F32vec4
# define GOOD_ALIGN 16
# define NUM_FLOATS 4
#else
#error “Choose the build target, please.”
#endif
// ベクトルレジスターに係数をロード
const FLOAT_VECTOR vec_c1(c1), vec_c2(c2);
// v[] のオフセットを GOOD_ALIGN バイト境界でアライメント
const int align_offset = (GOOD_ALIGN - ((uintptr_t)v) % GOOD_ALIGN)/ sizeof(float);
// スカラー事前ループ (最初の GOOD_ALIGN バイト境界でアライメントされていない要素)
#pragma loop count max(NUM_FLOATS-1)
for (int i=0; i< align_offset; i++) {
u[i] += c1* (v[i+ dx] + v[i- dx])
+ c2* (v[x+2*dx] + v[i-2*dx]);
}
// アライメントされているインテル® MIC ベクトルレジスター配列 – u と v は同じ境界でアライメントされると仮定
FLOAT_VECTOR * vec_v = (FLOAT_VECTOR*)(v+align_offset);
FLOAT_VECTOR * vec_u = (FLOAT_VECTOR*)(u+align_offset);
const int vec_loop_trip = (dx - align_offset) / NUM_FLOATS;
const int vec_dx = dx / NUM_FLOATS;
// インテル® MIC ベクトルレジスターに対するループ
for(int i=0; i<vec_loop_trip; i++) {
vec_u[i] += vec_c1* (vec_v[i+ vec_dx] + vec_v[i- vec_dx])
+ vec_c2* (vec_v[i+2*vec_dx] + vec_v[i-2*vec_dx]);
}
// スカラー・リマインダー・ループ (残りの要素)
#pragma loop count max(NUM_FLOATS-1)
for (int i=align_offset+NUM_FLOATS*vec_loop_trip; i<dx; i++) {
u[i] += c1* (v[i+ dx] + v[i- dx])
+ c2* (v[i+2*dx] + v[i-2*dx]);
}
図 3: マクロを使ってマシン固有の要素数やアライメント要件などを抽象化し、インテルの C++ SIMD クラスによりベクトル化されたループをすべてのインテル® アーキテクチャー向けに拡張したコード。インテル® Xeon® プロセッサーとインテル® MIC アーキテクチャー間の移植が容易になります。
これらのクラスを利用するインテル® アドバンスト・ベクトル・エクステンション (インテル® AVX) のような新しいハードウェア言語拡張に容易に移行することもできます (7、8)。データ・アライメントとレジスターごとの浮動小数点スカラーの数に C マクロ定義を用いてコードを一般化することで、インテル® MIC アーキテクチャー、インテル® AVX、インテル® ストリーミング SIMD 拡張命令 (インテル® SSE) 向けに再コンパイルできるようになります。
インテル® コンパイラーで生成されるベクトルコードによるアライメントの最適化
図 4 は、図 2 の実装に配列表記を使用したバージョンです。この実装では、__assume_aligned() 宣言を使ってインテル® コンパイラーにデータ・アライメント情報を伝える方法も示します。適切な最適化が行われた場合、コンパイラーにより生成されるベクトルコードは、組込みコードと同様に動作します。__assume_aligned(u,64) および __assume_aligned(v,64) 宣言は、配列 u と v の基本アドレスが 64 バイト境界でアライメントされることを示しています。別の実装として、__assume(<var> %16 == 0) 宣言を使用して、整数スカラー <var> が 16 の倍数であることを示すこともできます。この場合、v[i] のアドレスが 64 バイト境界でアライメントされているため、オフセットアドレス v[i+ <var>] も 64 バイト境界でアライメントされています。__assume() と __assume_aligned() の使用は必須ではありません。これらの宣言は、アライメント情報をコンパイラーに伝え、コンパイラーによるコード生成を最小限に抑えるための手段です。
// 配列 u と v[k*dx] (k=-2、..、2) は 64 バイト境界でアライメントされていると仮定
__assume_aligned(u,64);
__assume_aligned(v,64);
float* v_pdx = &(v[ dx]); __assume_aligned(v_pdx, 64);
float* v_mdx = &(v[ -dx]); __assume_aligned(v_mdx, 64);
float* v_p2dx = &(v[ 2*dx]); __assume_aligned(v_p2dx,64);
float* v_m2dx = &(v[-2*dx]); __assume_aligned(v_m2dx,64);
const int vec_loop_trip = dx/16;
// ベクトルレジスターを使用するループ (16 の単精度浮動小数点値)
for(int i=0; i<vec_loop_trip; i=+16) {
u[i:16] += c1* (v_pdx [i:16] + v_mdx [i:16])
+ c2* (v_p2dx[i:16] + v_m2dx[i:16]);
}
図 4: インテル® Cilk™ Plus の配列表記により明示的にベクトル化されたループの実装例。この例では、すべての配列が 64 バイト境界でアライメントされており、ループの反復数が 16 の倍数であるため、コンパイラーはアライメントされたロードとストアのみを生成してリマインダー・ループは生成しません。
図 4 のコードも、図 3 の C マクロを使って、インテル® MIC アーキテクチャーとすべてのインテル® Xeon® プロセッサー・ファミリーをサポートするように書き換えられます。
アライメント情報は、プラグマ/宣言子でコンパイラーに知らせることもできます。すべての配列がアライメントされているかどうか分からない場合、図 5 の Fortran コード例のように、プラグマ/宣言子を使ってアライメントされている配列を示すことができます。
integer n
real v(*), w(*), u(*)
!dir$ ASSUME_ALIGNED v:64, w:64
do i=1,n
v(i) = u(i)
w(i) = 5.0 * u(i)
enddo
図 5: ASSUME_ALIGNED 宣言子により配列 v と w のヒントを提供する Fortran コード例。この場合、配列 u のみアライメントされていないアクセスが必要になります。
より現実的な 3 次元ステンシルの例
ここでは、3 次元配列 v の 2 次元に適用される単純な 9 点有限差分演算の 3 つのバージョンのパフォーマンスを比較します。図 6 は v の有限差分を計算する単純な C 実装例、図 7 は配列のアライメントを明示的に処理する実装例、図 8 は C++ ベクトルクラスを使用する実装例です。
#pragma simd
for (int i=0; i<dx; i++) {
u[i] += c1* (v[i+ dx] + v[i- dx]) + c2* (v[i+2*dx] + v[i-2*dx])
+ c3* (v[x+3*dx] + v[i-3*dx]) + c4* (v[x+4*dx] + v[i-4*dx]);
}
図 6: 3 次元配列 v の 2 次元に対する 9 点有限差分の単純な C 実装例
const int align_offset = (GOOD_ALIGN - ((uintptr_t)v) % GOOD_ALIGN)/ sizeof(float);
#pragma loop count max(NUM_FLOATS-1)
for (int i=0; i< align_offset; i++) {
u[i] += c1* (v[i+ dx] + v[i- dx]) + c2* (v[x+2*dx] + v[i-2*dx])
+ c3* (v[x+3*dx] + v[i-3*dx]) + c4* (v[x+4*dx] + v[i-4*dx]);
}
float * aligned_v = (float*)(v+align_offset);
float * aligned_u = (float*)(u+align_offset);
const int vec_loop_trip = (dx - align_offset) / NUM_FLOATS;
#pragma vector aligned
#pragma simd
for (int i=0; i<vec_loop_trip*NUM_FLOATS; i++) {
aligned_u[ix] += c1* (aligned_v[i+ dimx] + aligned_v[i- dimx])
+ c2* (aligned_v[i+2*dimx] + aligned_v[i-2*dimx])
+ c3* (aligned_v[i+3*dimx] + aligned_v[i-3*dimx])
+ c4* (aligned_v[i+4*dimx] + aligned_v[i-4*dimx]);
}
#pragma loop count max(NUM_FLOATS-1)
for (int i=align_offset+NUM_FLOATS*vec_loop_trip; i<dx; i++) {
u[i] += c1* (v[i+ dx] + v[i- dx]) + c2* (v[i+2*dx] + v[i-2*dx])
+ c3* (v[x+3*dx] + v[i-3*dx]) + c4* (v[x+4*dx] + v[i-4*dx]);
}
図 7: 配列のアライメントを明示的に処理する 3 次元配列 v の 2 次元に対する 9 点有限差分の実装例
#include <immintrin.h>
#define PFTCH1(addr, DIST) _mm_prefetch((char const*) ((addr)+(DIST)), _MM_HINT_T0);
#define PFTCH2(addr, DIST) _mm_prefetch((char const*) ((addr)+(DIST)), _MM_HINT_T1);
#define L1_DIST 4
#define L2_DIST 16
#define PREFETCH(addr)
PFTCH1((addr), (L1_DIST))
PFTCH2((addr), (L2_DIST))
const int align_offset = (GOOD_ALIGN - ((uintptr_t)v) % GOOD_ALIGN)/ sizeof(float);
#pragma loop count max(NUM_FLOATS-1)
for (int i=0; i< align_offset; i++) {
u[i] += c1* (v[i+ dx] + v[i- dx]) + c2* (v[x+2*dx] + v[i-2*dx])
+ c3* (v[x+3*dx] + v[i-3*dx]) + c4* (v[x+4*dx] + v[i-4*dx]);
}
const FLOAT_VECTOR vec_c1(c1), vec_c2(c2), vec_c3(c3), vec_c4(c4);
FLOAT_VECTOR * vec_v = (FLOAT_VECTOR*)(v+align_offset);
FLOAT_VECTOR * vec_u = (FLOAT_VECTOR*)(u+align_offset);
const int vec_loop_trip = (dx - align_offset) / NUM_FLOATS;
const int vec_dx = dx / NUM_FLOATS;
#pragma noprefetch
for(int i=0; i<vec_loop_trip; i++) {
PREFETCH(&vec_u[i])
PREFETCH(&vec_v[i+ dimx]) PREFETCH(&vec_v[i- dimx])
PREFETCH(&vec_v[i+2*dimx]) PREFETCH(&vec_v[i-2*dimx])
PREFETCH(&vec_v[i+3*dimx]) PREFETCH(&vec_v[i-3*dimx])
PREFETCH(&vec_v[i+4*dimx]) PREFETCH(&vec_v[i-4*dimx])
vec_u[i] += vec_c1*vec_v[i+ vec_dx] + vec_c1*vec_v[i- vec_dx]
+ vec_c2*vec_v[i+2*vec_dx] + vec_c2*vec_v[i-2*vec_dx]
+ vec_c3*vec_v[i+3*vec_dx] + vec_c3*vec_v[i-3*vec_dx]
+ vec_c4*vec_v[i+4*vec_dx] + vec_c4*vec_v[i-4*vec_dx];
}
#pragma loop count max(NUM_FLOATS-1)
for (int i=align_offset+NUM_FLOATS*vec_loop_trip; i<dx; i++) {
u[i] += c1* (v[i+ dx] + v[i- dx]) + c2* (v[i+2*dx] + v[i-2*dx])
+ c3* (v[x+3*dx] + v[i-3*dx]) + c4* (v[x+4*dx] + v[i-4*dx]);
}
図 8: C++ ベクトルクラスを使用する 3 次元配列 v の 2 次元に対する 9 点有限差分の実装例。この例は、C プリフェッチ組込み関数により、配列の 1 次元 (L1) および 2 次元 (L2) のプリフェッチを直接制御する方法も示しています。
テストでは、各バージョンを単一のインテル® MIC アーキテクチャー・コア上でシングルスレッドで実行し、ベクトル化の違いを検証しました。これは、3 つの実装例の違いを識別する統合テストです。実際のシナリオでは、コードの並列実装で最適化の違いをテストすべきです。パフォーマンスの向上は、ベースライン・バージョン (図 6) と配列アライメント (図 7) および C++ ベクトルクラス (図 8) のバージョンを比較して測定しました。C++ ベクトルクラスを使用するバージョンでは、C プリフェッチ組込み関数を明示的に呼び出して、配列 vec_u と vec_v の 1 次元 (L1) と第 2次元 (L2) のプリフェッチを制御しています。
テストでは、配列 u と v の次元を dx=464、dy=224、dz=840 とし、コードはインテル® C/C++ コンパイラー 14.0.0.080 でビルドして、インテル® Xeon Phi™ 7120 コプロセッサー上でシングルスレッドのテストを行いました。入力配列の各ポイントに対して、10 反復の 9 点有限差分操作が適用されました。表 1 に、32 バイト境界および 64 バイト境界でアライメントされた配列を使用した場合の 3 つのバージョンの実行時間を秒単位で示します。どのバージョンでも、インテル® MIC アーキテクチャーの 512 ビットのベクトルレジスターと同じ境界で配列をアライメントし、その情報を伝えることでパフォーマンスが 23% 以上も向上しました。
表 1: 3 つのバージョンのシングルスレッドでの実行時間 (秒単位)。配列 v と u を 32 バイトまたは 64 バイト境界でアライメントした場合の結果です。最後の行は、配列のアライメント境界を 32 バイトから 64 バイトに変更した場合のパフォーマンスの向上を示しています。

表 1 から、3 つのバージョンのパフォーマンスの違いも分かります。C++ ベクトルクラス・バージョンと比べると、ベースライン・バージョンは 50% (32 バイト境界の場合) ~ 70% (64 バイト境界の場合) 遅く、配列アライメント・バージョンは 13% (64 バイト境界の場合) 遅いことが分かります。その大きな要因の 1 つは、図 8 の C++ ベクトルクラス・バージョンでは、C プリフェッチ組込み関数により配列の 1 次元 (L1) と 2 次元 (L2) をコードで明示的に制御しているためです。次に、インテル® コンパイラーの機能を利用して、ベースライン・バージョンと配列アライメント・バージョンでデータ・プリフェッチを制御してみましょう。
インテル® コンパイラーは、インテル® MIC アーキテクチャー向けにプリフェッチの距離を指定するグローバルオプションを提供しています。
-opt-prefetch-distance=n1[,n2] n1 は L1 から L2 へのプリフェッチの距離を指定します。 n2 は L2 から L1 (n2<=n1) へのプリフェッチの距離を指定します。
表 2 は、-opt-prefetch-distance=8,2 コンパイラー・オプションを指定して、配列 v と u のプリフェッチの距離を制御した実行バイナリーのテスト結果です。プリフェッチの制御により、配列アライメント・バージョンでも C++ ベクトルクラス・バージョンと同様のパフォーマンスが得られました。また、ベースライン・バージョンも、C++ ベクトルクラス・バージョンと比べると、まだ 8% (32 バイト境界の場合) ~ 14% (64 バイト境界の場合) 遅いものの、パフォーマンスが向上しました。64 バイト境界でアライメントすることで、すべてのバージョンで約 30% のパフォーマンス向上を達成できることが分かります。
表 2: -opt-prefetch-distance=8,2 オプションで L2 から L1 へのプリフェッチの距離を指定してコンパイルした場合の 3 つのバージョンのシングルスレッドでの実行時間 (秒単位)。配列 v と u を 32 バイトまたは 64 バイト境界でアライメントした場合の結果です。最後の行は、配列のアライメント境界を 32 バイトから 64 バイトに変更した場合のパフォーマンスの向上を示しています。

インテル® コンパイラーは、プリフェッチ・コードの生成を制御するさまざまな機能を提供しています。例えば、次のように prefetch プラグマを使ってプリフェッチ要求を発行できます。
C ループの場合:
#pragma prefetch var:hint:distance
Fortran ループの場合:
CDEC$ prefetch var:hint:distance
プリフェッチに関する詳細は、インテル® コンパイラーのドキュメントを参照してください。インテル® Xeon Phi™ コプロセッサーのコンパイラー・プリフェッチに関する詳細は、参考文献 (8) を参照してください。
まとめ
SIMD ベースのデータ並列処理を最大限に利用するためには、効率良いベクトル化が重要です。インテル® コンパイラーは、最適化されたベクトル命令を生成するさまざまな機能を提供しています。高レベルのコードは自動ベクトル化、インテル® Cilk™ Plus 拡張、OpenMP* 4.0 を利用して、専用の構文や移植性に優れた OpenMP* などの一般的な標準規格により、多くのコードをベクトル化できます。これらの高レベルのアプローチは効率良いベクトルコードを生成し、実装と保守が簡単で、移植性に優れているため、効果の高いベクトル化を行う方法として推奨されています。場合によっては、限定されたコード領域でアプリケーションの計算時間の大半が費やされており、パフォーマンスを最大限に引き出すことが重要なこともあるでしょう。そのような場合であっても、SIMD ベクトルクラスは、高レベルのコードのように使用でき、組込み関数/アセンブリー・コードと同様のパフォーマンスをもたらします。組込み関数やアセンブリー・コードによる低レベルのコードは、保守コストに見合うパフォーマンス向上が得られる小さなコード領域のみに限定すべきです。
参考文献
1. マルチコア・プロセッサーにおける 3 次元有限差分法の実装: https://www.isus.jp/article/parallel-special/3d-finite-differences/
2. OpenMP* 4.0 仕様: http://www.openmp.org (英語)
3. インテル® Cilk™ Plus のサポート: https://www.isus.jp/article/intel-cilk-plus/
4. インテル® C++ コンパイラーによる自動ベクトル化: https://www.isus.jp/article/compileroptimization/guide-to-auto-vectorization/
5. インテル® コンパイラー 13 最適化クイック・リファレンス・ガイド: http://software.intel.com/sites/default/files/Compiler_QRG_2013.pdf (英語)
6. インテル® C++ 組込み関数リファレンス: http://software.intel.com/sites/products/documentation/studio/composer/en-us/2011/compiler_c/intref_cls/common/intref_bk_intro.htm (英語)
7. インテル® アドバンスト・ベクトル・エクステンション (インテル® AVX): http://software.intel.com/en-us/avx
8. インテル® Xeon Phi™ コプロセッサーのコンパイラー・プリフェッチ: http://software.intel.com/sites/default/files/managed/5d/f3/5.3-prefetching-on-mic-4.pdf (英語)
著者紹介
Leonardo Borges、Hideki Saito、Philippe Thierry は、インテルのソフトウェア & ソリューション・グループに所属しています。
Intel、インテル、Intel ロゴ、Cilk、Xeon、Xeon Phi は、アメリカ合衆国および / またはその他の国における Intel Corporation の商標です。
* その他の社名、製品名などは、一般に各社の表示、商標または登録商標です。
© 2012 Intel Corporation. 無断での引用、転載を禁じます。
* パフォーマンスおよびベンチマークの結果に関する詳細は、www.intel.com/benchmarks (英語) を参照してください。
コンパイラーの最適化に関する詳細は、最適化に関する注意事項を参照してください。


